Понятие системы и ее розвязків
Определение: Если ставится задача найти все общие развязки двух (или более) уравнений с одной или несколькими переменными, то говорят, что надо розвязати систему уравнений.
Определение: Розвязком системы — такое значение переменной или такой упорядоченный набор значений зміниих, что удовлетворяет сразу всем уравнениям системы, то есть розвязком системы двух или более уравнений с  неизвестными называется такое упорядоченное множество множество
неизвестными называется такое упорядоченное множество множество  чисел, при подстановке которых в систему вместо неизвестных все уравнения превращаются в верные числовые равенства.
чисел, при подстановке которых в систему вместо неизвестных все уравнения превращаются в верные числовые равенства.
Определение: Розвязати систему уравнений — найти все ее развязки или доказать, что их нет.
Если система не имеет решения, то она несовместима.
Примеры систем
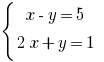 — система двух уравнений с двумя переменными
— система двух уравнений с двумя переменными
Пара 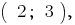 то есть
то есть 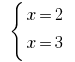 —решение системы
—решение системы
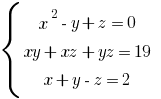 — система трех уравнений с тремя переменными
— система трех уравнений с тремя переменными
Тройка 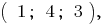 то есть
то есть 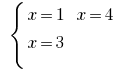 — один из розвязків системы
— один из розвязків системы
Схема решению систем уравнений
Графический метод
- Выполняем равносильные преобразования, так, чтобы было удобно построить график функции. Например:
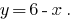
- Строим графики.
- Находим точки пересечения графиков. Координаты этих точек и есть розвязком данной системы уравнений.
Метод подстановки
- Из одного уравнения системы выражаем одну переменную через другую, всегда выбираем удобную переменную. Например, из уравнения
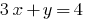 выражаем переменную
выражаем переменную 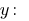
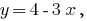 а не наоборот.
а не наоборот. - Найденное значение подставляем в другое уравнение системы и получаем уравнение с одной переменной.
- Розвязуємо полученное уравнение
- Найденное значение подставляем в выраженное уравнение, и находим значение второй переменной.
Метод сложения
- Урівнюємо коэффициенты при одной из переменных путем по членного умножения обоих уравнений на множители, подобранные соответствующим образом.
- Добавляем (или отнимаем) почленно два уравнения системы, тем самым исключается одна переменная.
- Розвязуємо полученное уравнение.
- Подставляем найденное значение переменной в любое из исходных уравнений.
Примеры решению систем уравнений
Решению графическим методом
Пример 1
Розвяжіть уравнения: 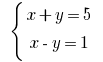
Решения:
Строим графики 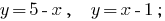
Построив графики увидим, что графики пересекаются в точке 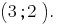
Ответ: 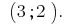
Решению методом подстановки
Пример 2
Розвяжіть уравнения: 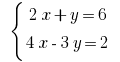
Решения:
Из первого уравнения выражаем 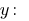
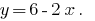 А полученное выражение подставляем во второе уравнение системы:
А полученное выражение подставляем во второе уравнение системы:
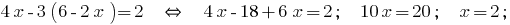
Полученное значение  подставляем в выражение
подставляем в выражение 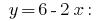
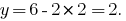
Ответ: 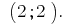
Решению методом добавления
Пример 3
Розвяжіть уравнения: 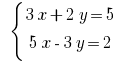
Решения:
Должны избавиться от переменной 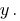 Умножаем почленно первое уравнение системы на 3, а второе – на 2.
Умножаем почленно первое уравнение системы на 3, а второе – на 2.
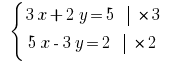
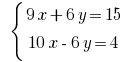
Добавляем почленно уравнение и получаем: 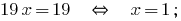
Находим значение  из первого уравнения системы:
из первого уравнения системы: 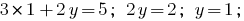
Ответ: 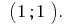
Замечание: В методе добавления можно умножать не только на положительные числа, а и на отрицательные.
Каким способом розвязувати систему уравнений решать только Вам.

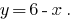
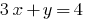 выражаем переменную
выражаем переменную 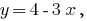 а не наоборот.
а не наоборот.