- Пользуясь непрерывностью функции
 , пробуем подставить значения
, пробуем подставить значения  в функцию
в функцию 
- Если вычисляется предел при
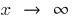 , то пробуем в числителе и местоимении вынести за скобки наивысший степень неизвестного
, то пробуем в числителе и местоимении вынести за скобки наивысший степень неизвестного - Если в результате подстановки
 получили выражение типа
получили выражение типа 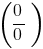 , то
, то
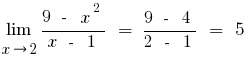
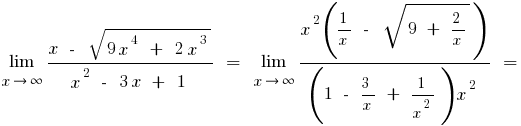
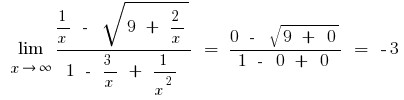
а) пробуем разложить числитель и местоимение на множители
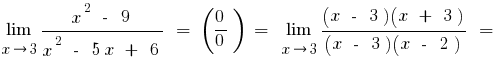
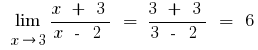
б) если числителя или знаменателя входят выражения с квадратным или кубическим корнем, то умножаем числитель и знаменатель на соответствующие выражения, чтобы избавиться от заданных корней (иногда вводят замену и выражение с корнем обозначают новой переменной)
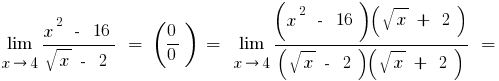
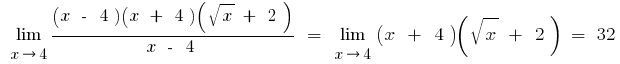
в) если под знаком предела стоят тригонометрические или обратные тригонометрические функции, то такие границы сводят к первой выдающейся границы

или ее вариаций



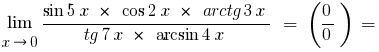
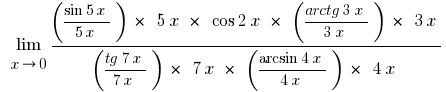
Сократив числитель и знаменатель на переменные, стоящие за скобками, учитывая, что 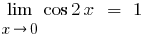 , и учитывая перщу выдающуюся границу и ее вариации, получаем
, и учитывая перщу выдающуюся границу и ее вариации, получаем 
Если у вас есть вопросы по решению задач по математике, вы можете воспользоваться сайтом urokam.net.

 , пробуем подставить значения
, пробуем подставить значения  в функцию
в функцию 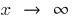 , то пробуем в числителе и местоимении вынести за скобки наивысший степень неизвестного
, то пробуем в числителе и местоимении вынести за скобки наивысший степень неизвестного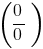 , то
, то