Определение:Если функция 
определена на отрезке 
и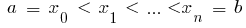 
, то определенным интегралом от функции на отрезке называется число, равное предела интегральной суммы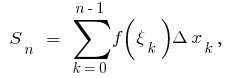 
где 
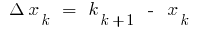, f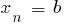 
то есть
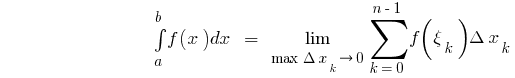
где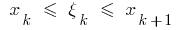 
i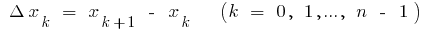 
Построение интегральной суммы на примере определения площади криволинейной трапеции
Пусть на отрезке задано неотъемлемою и непрерывную функцию
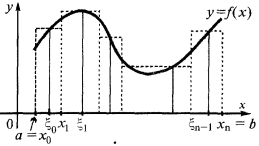
Чтобы определить площадь криволинейной трапеции (ограниченной кривой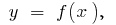 
осью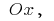 
и прямыми, 
и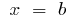 
), разбиваем отрезок точками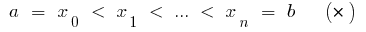 
на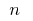 
частей, выбираем на каждом из полученных частичных отрезков 
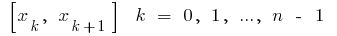произвольную точку 
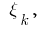вычисляем значения
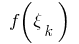функции в этих точках и составляем сумму 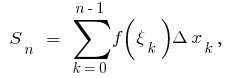где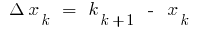
Эта сумма равна сумме площадей заштрихованных прямоугольников и называется интегральной суммой.
Если теперь число точек разбиения неограниченно увеличивается и длина максимального (наибольшего) частичного отрезка разбиения стремится к нулю, и при этом величина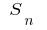 
стремится к определенной границы 
не зависит от способа разбиения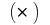 
и выбора точек 
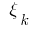на частичных отрезках, то величину 
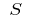называют площадью криволинейной трапеции, т. е.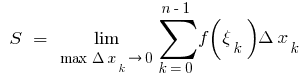 
Формула Ньютона - Лейбница
Если функция определена и непрерывна на отрезке и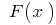 
— ее первообразная (то есть 
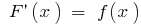), то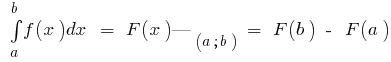 
Пример. Поскольку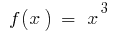 
одна из первобытных 
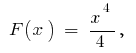то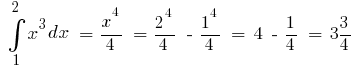 
Основные свойства определенного интеграла
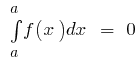
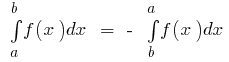
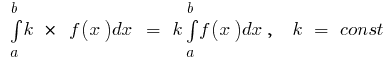
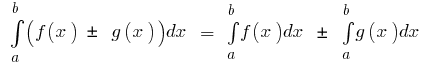
- Если
интегрированная на 
и 
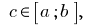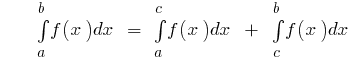
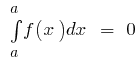
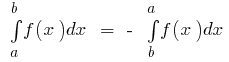
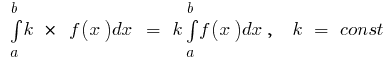
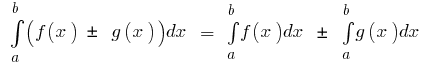
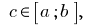то
то