واضح لا يتجزأ

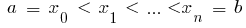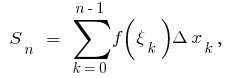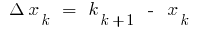تعريف:إذا كانت وظيفة محددة على فترة ومن ثم واضح لا يتجزأ من وظيفة على فاصل هو عدد يساوي الحد لا يتجزأ من المبلغ حيث f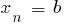

هذا هو

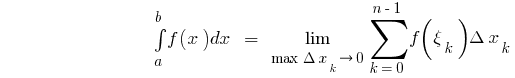
حيث 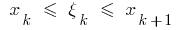أنا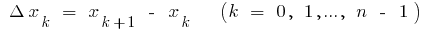

بناء لا يتجزأ من مبالغ على سبيل المثال تحديد منطقة منحنية شبه منحرف

دعونا في هذا الجزء هو مجموعة متكاملة ومستمرة وظيفة

 

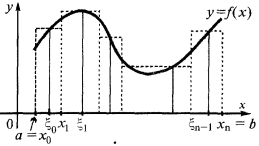
لتحديد منطقة منحنية شبه منحرف (يحدها المنحنى 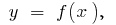على المحور 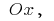مباشرة و 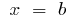) ، تقسيم قطع نقاط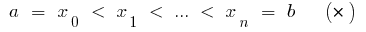

على 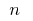أجزاء مختارة على كل من حصل على جزئية قطاعات 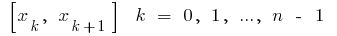التعسفي نقطة من 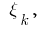القيم المحسوبة 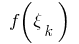من وظيفة في هذه النقاط تشكل مجموع 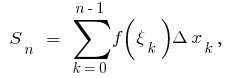فيها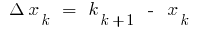

هذا المبلغ يساوي مجموع مناطق مظللة مستطيلات يسمى جزءا لا يتجزأ من المبلغ.

إذا الآن عدد من تقسيم النقاط يزيد إلى أجل غير مسمى ، وطول ماكس (أعلى) قطع جزئي التقسيم يميل إلى الصفر ، والقيمة 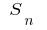يميل إلى حد معين لا تعتمد على طريقة تقسيم 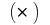واختيار النقاط 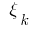على جزئية شرائح ، ثم قيمة 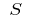يسمى منطقة منحنية شبه منحرف ، أي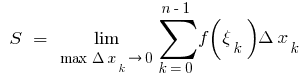

صيغة نيوتن ليبنيز

إذا كانت الوظيفة المحددة المستمر على الفاصل و 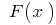هو جزء لا يتجزأ من (أي 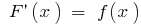) ، ثم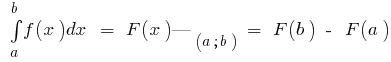

على سبيل المثال. باعتبارها 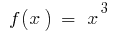واحدة من البدائية 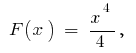ثم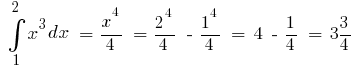

الخصائص الأساسية واضح لا يتجزأ

1. 
2. 
3. 
4.  
5. 
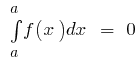
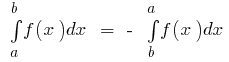
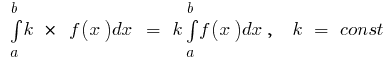
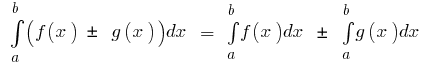
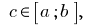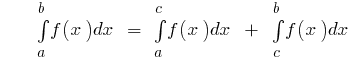
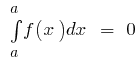
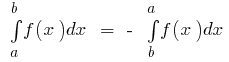
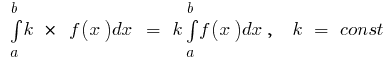
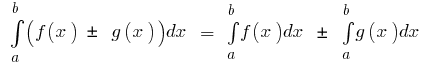
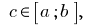6. إذا متكاملة على و ثم