Означення:Якщо функція 
визначена на відрізку 
і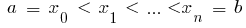 
, то визначеним інтегралом від функції на відрізку називається число, що дорівнює границі інтегральної суми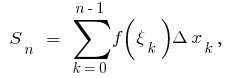 
де 
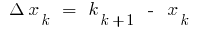, f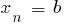 
тобто
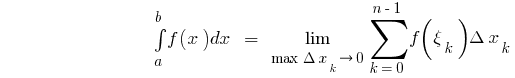
де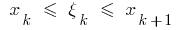 
i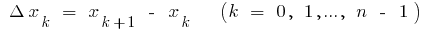 
Побудова інтегральної суми на прикладі визначення площі криволінійної трапеції
Нехай на відрізку задано невідємну і неперервну функцію
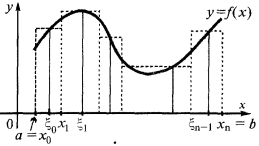
Щоб визначити площу криволінійної трапеції (обмеженої криво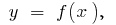ю 
віссю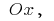 
прямими 
і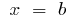 
), розбиваємо відрізок точками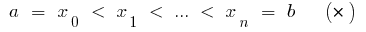 
на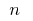 
частин, вибираємо на кожному з одержаних часткових відрізків 
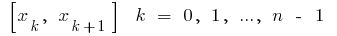довільну точку 
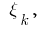обчислюємо значення
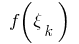функції в цих точках і складаємо суму 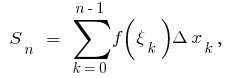де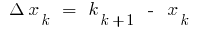
Ця сума дорівнює сумі площ заштрихованих прямокутників і називається інтегральною сумою.
Якщо тепер число точок розбиття необмежено збільшується і довжина максимального (найбільшого) часткового відрізка розбиття прямує до нуля, і при цьому величина 
прямує до певної границі 
що не залежить від способу розбиття 
і вибору точок 
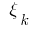на часткових відрізках, то величину 
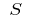називають площею криволінійної трапеції, тобто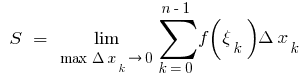 
Формула Ньютона - Лейбніца
Якщо функція визначена і неперервна на відрізку і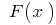 
— будь-яка її первісна (тоб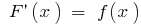то 
), то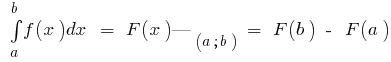 
Приклад. Оскільки для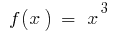 
одна з первісних 
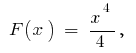то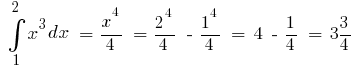 
Основні властивості визначеного інтеграла
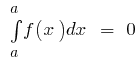
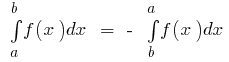
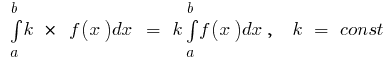
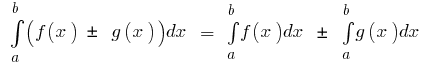
- Якщо
інтегрована на 
і 
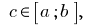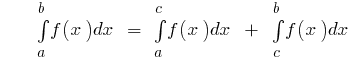
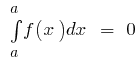
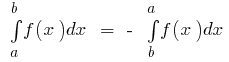
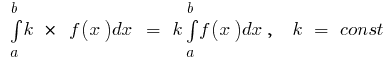
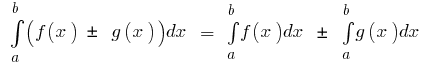
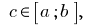то
то