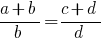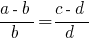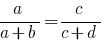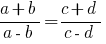Пропорції і відношення, пряма та обернена пропорційність

Означення: Пропорцією називається рівність двох відношень.

або .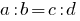

Основна властивість пропорцій

Добуток крайність членів членів пропорції дорівнює добутку її середніх членів: якщо

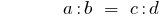, то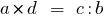

Властивості пропорцій

1. Добуток крайність членів членів пропорції дорівнює добутку її середніх членів: .
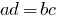2. Кожний крайній член пропорції дорівнює добутку її середніх членів поділеному на інший крайній член.
3. У кожній пропорції можна поміняти місцями або лише середні члени, або лише крайні, або і ті, й інші одночасно.

Приклад знаходження пропорції в математиці

Якщ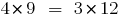о , то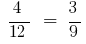

В пропорції 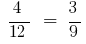змінемо місцями середні члени або крайні члени, тоді отримаємо знову правильні рівност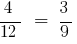і:

і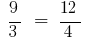

Похідні пропорції

Якщо задана пропорція 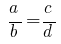, то 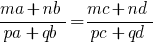, що називається похідною пропорцією.

Найчастіше вживані похідні пропорції

• 
• 
• 
• 

Масштаб

Означення: Масштаб — відношення відстані на карті до відповідної відстані на реальній місцевості.

Прямо пропорційні величини

Означення: Дві величини називаються прямо пропорційними, якщо зі збільшенням значень однієї з них кілька разів значення другої збільшується у стільки ж разів.

Задача на прямо пропорційні величини

Сторона квадрата дорівнює 3 дм. Як зміниться периметр квадрата, якщо його сторону збільшити в 3 рази, в 4 рази, в 5 разів?

Сторона квадрата 3 дм, периметр 12 дм

Сторона квадрата 9 дм, периметр 36 дм

Сторона квадрата 12 дм, периметр 48 дм

Сторона квадрата 15 дм, периметр 60 дм

При збільшенні сторони квадрата в 3 рази (була 3 дм, стала — 9 дм), периметр збільшився також в 3 рази (був 9 дм, став — 36 дм).

Аналогічно, при збільшенні сторони квадрата в 4 рази (була 3 дм, стала — 12 дм), периметр збільшився також в 4 рази (був 12 дм, став — 48 дм).

Висновок: при збільшенні сторони квадрата в кілька разів, периметр збільшується в стільки ж разів.

Сторона квадрата прямо пропорційна його периметру.

Обернено пропорційні величини

Означення: Дві величини називаються обенено пропорційними, якщо зі збільшенням значень однієї з них кілька разів значення другої зменшується у стільки ж разів.

Задача на обернено пропорційні величини

Відстань між двома селищами дорівнює 160 км. За який час можна доїхати з одного селища до іншого, якщо швидкість 10 км/год збільшити в 2 рази, 4 рази, в 8 рази?

Швидкість, км/год 10, час, год 16

Швидкість, км/год 20, час, год 8

Швидкість, км/год 40, час, год 4

Швидкість, км/год 80, час, год 2

При збільшенні швидкості в 2 рази (була 10 км/год, стала — 20 км/год), час скоротився (зменшився) в 2 рази (було 16 год, стало — 8 год).

Аналогічно, при збільшенні швидкості в 4 рази (була 10 км/год, стала — 40 км/год), час скоротився (зменшився) в 4 рази (було 16 год, стало — 4 год).

Висновок: при збільшенні швидкості в кілька разів, час зменшується у стільки ж разів.

Швидкість обернено пропорційна часу.

Числа 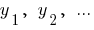пропорційні числам 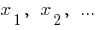, якщо 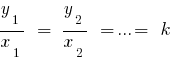— коефіцієнт пропорційності.
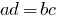