Неперервність функції у точці
Означення: Функція  називається неперервною в точці
називається неперервною в точці 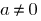 , якщо при
, якщо при 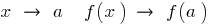 , тобто
, тобто 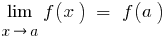 .
.
Неперервність функції на проміжку
Означення: Якщо функція  неперервна в кожній точці деякого проміжку
неперервна в кожній точці деякого проміжку  , то її називають неперервною на проміжку
, то її називають неперервною на проміжку  .
.
Властивості неперервності функції
Приклад неперервності функції
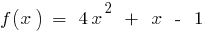 — неперервна функція (многочлен)
— неперервна функція (многочлен)
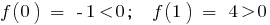 , тому на інтервалі (0;1) існує точка
, тому на інтервалі (0;1) існує точка  , в якій функція дорівнює 0:
, в якій функція дорівнює 0: 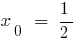
Приклад неперервності функції
Приклад неперервності функції
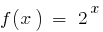 — неперервна функція. Якщо
— неперервна функція. Якщо
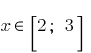 , то
, то 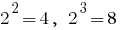 . Оскільки
. Оскільки 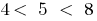 , то існує точка
, то існує точка  , в якій
, в якій 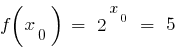 .
.
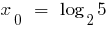
Правило знаходження найбільшого і найменшого значенб функції.
- Якщо неперервна на відрузку
 функці набуває на кінцях цього відрізка значень різних знаків, то в деякій точці цього відрізка вона набуває значення, яке дорівнює нулю.
функці набуває на кінцях цього відрізка значень різних знаків, то в деякій точці цього відрізка вона набуває значення, яке дорівнює нулю. - Якщо на інтервалі
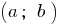 функція
функція  неперервна і не перетворюється на нуль, то на цьому інтервалі функція зберігає постійний знак.
неперервна і не перетворюється на нуль, то на цьому інтервалі функція зберігає постійний знак. - Функція
 , яка неперервна на відрізку
, яка неперервна на відрізку  , набуває всіх проміжних значень між значеннями цієї функції у крайніх точках, тобто між
, набуває всіх проміжних значень між значеннями цієї функції у крайніх точках, тобто між 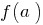 і
і 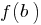 .
. - Функція
 , яка неперервна на відрізку
, яка неперервна на відрізку  , обмежена на цьому відрізку, тобто існують два числа
, обмежена на цьому відрізку, тобто існують два числа  і
і  , що для всіх
, що для всіх 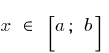 виконується нерівність
виконується нерівність 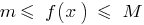 .
. - Сума різниці і добуток неперервних на даному інтервалі функцій — неперервна на тому ж самому інтервалі функція. Частка двох неперервних функцій — неперервна функція в усіх точках, в яких знаменник не перетвоюється на нуль.
- Функція, обернена до неперервної функції на заданому інтервалі, є неперервною на цьому інтервалі.
- Якщо функція
 має похідну в точці
має похідну в точці  , то вона є неперервною в цій точці.
, то вона є неперервною в цій точці.
Точки розриву
Означення: Точка  точка розриву функції
точка розриву функції 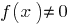 , якщо в точці
, якщо в точці  , не виконується умова, що при
, не виконується умова, що при 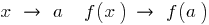 .
.
Приклади функцій, що містять точки розриву
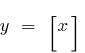 — точки розриву усі цілочислові точки
— точки розриву усі цілочислові точки
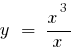 — точка розриву - 0
— точка розриву - 0
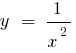 — точка розриву - 0
— точка розриву - 0

 функці набуває на кінцях цього відрізка значень різних знаків, то в деякій точці цього відрізка вона набуває значення, яке дорівнює нулю.
функці набуває на кінцях цього відрізка значень різних знаків, то в деякій точці цього відрізка вона набуває значення, яке дорівнює нулю.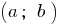 функція
функція 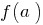 і
і 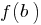 .
. і
і  , що для всіх
, що для всіх 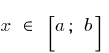 виконується нерівність
виконується нерівність 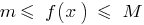 .
.