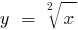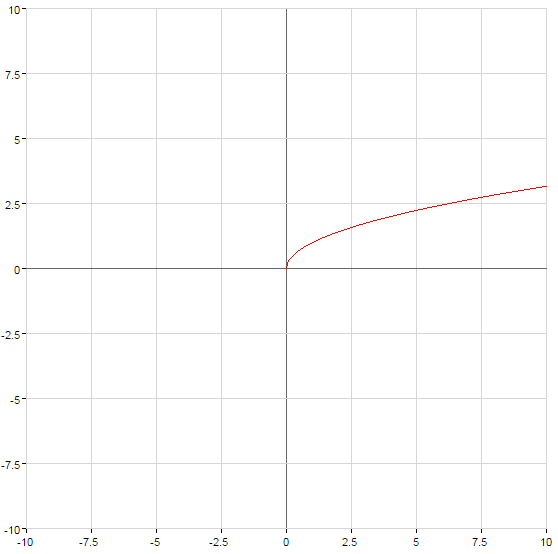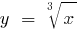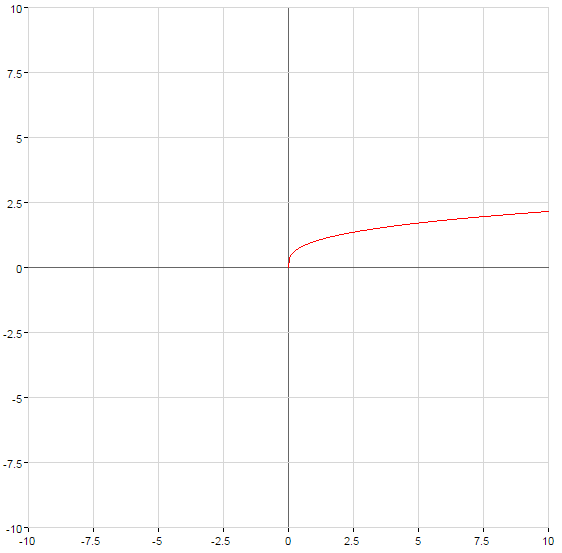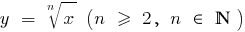
Властивості функцій кореня
n — парне 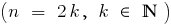
 n — непарне
n — непарне 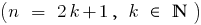

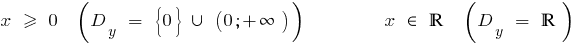
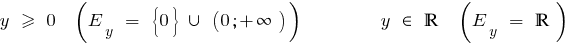
ні парна, ні непарна непарна
непарна
Якщо 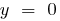 , то
, то 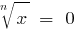 , тобто
, тобто 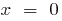 , отже, графік проходить через початок координат
, отже, графік проходить через початок координат
Функція неперервна в кожній точці своєї області і при 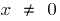 має похідну
має похідну 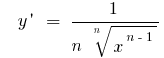
Функція зростає на всій своїй області визначення
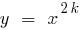 (при
(при 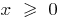 ) i
) i 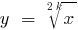

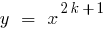 (при
(при 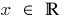 ) i
) i 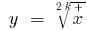
Графіки симетричні відносно прямої 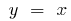
- Область визначення

- Множина значення

- Парність, непарність
- Точки перетину з осями координат
- Неперервність і диференційовність
- Зростання і спадання
- Взаємно обернені функції
Графіки функцій кореня