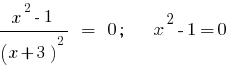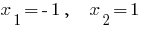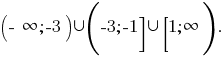Розвязування нерівностей за допомогою рівносильних перетворень
- Перетворення, що гарантують збереження правильної рівності
- Перевірка коренів підстановкою в початкову нерівність
Розвязування рівнянь за допомогою методу інтервалів
- Знайти ОДЗ.
- Знайти нулі функції:

- Позначити нулі на ОДЗ і знайти знак функції f(x) у кожному проміжку, на які розбиваються ОДЗ.
- Записати відповідь, ураховуючи знак заданої нерівності.
Розвязування нерівностей. Метод інтервалів.
- Знайти ОДЗ.
- Знайти нулі функції:

- Позначити нулі на ОДЗ і знайти знак функції f(x) у кожному проміжку, на які розбиваються ОДЗ.
- Записати відповідь, ураховуючи знак заданої нерівності.
Приклад 1.
Розвяжіть нерівність: 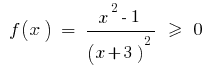
Розвязання. Нехай 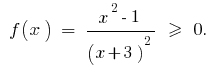
- ОДЗ:
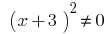 , отже
, отже 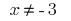 .
. - Нулі функції:

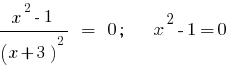
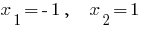
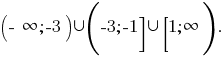
Приклад 2.
Указати найменше ціле число, яке є розвязком нерівності
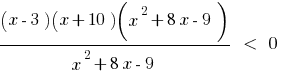
Розвязання. Розвяжемо дану нерівність методом інтервалів.
ОДЗ: 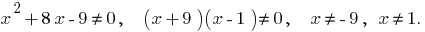
Знайдемо нулі функції: 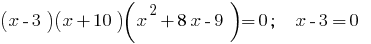 або
або 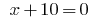
Тоді 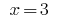 або
або 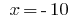 .
.
Зображуємо нулі та ОДЗ і знаходимо знак функції на кожному проміжку.
Тоді, розвязок даної нерівності 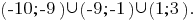 Отже, найменше ціле число, яке є розвязком даної нерівності, є число
Отже, найменше ціле число, яке є розвязком даної нерівності, є число 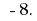
Відповідь: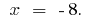


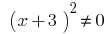 , отже
, отже 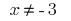 .
.