Крім натуральних чисел та нуля, існують інші числа - дробові. Коли один предмет ділять ( яблуко, торт, аркуш паперу ) або одиниці виміру ( метр, кілограм, градус ) ділять на рівні частини, виникають дробові числа.
Половина, чверть, третина, одна сота — це приклади дробових чисел.
Означення: Звичайний дріб (або простий дріб)– це число представлене у вигляді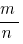 
, де 
- ціле, а 
- натуральне.
Записи виду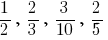 
— звичайні дроби, або коротше просто дроби.
Чисельник дробу — число, яке записане над рискою дробу.
Знаменник дробу — число, яке записане під рискою дробу.
Знаменник дробу показує на скільки рівних частин поділили щось ціле. А чисельник дробу показує скільки таких частин взяли.
Основна властивість дробів
Якщо чисельник і знаменник дробу помножити або поділити на однакову величину, що не дорівнює нулю, то буде отримано дріб рівний початковому, хоч дроби - різні.
Наприклад,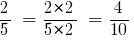 
І, навпаки,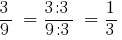 
Правильні та неправильні дроби
Чи може чисельник дорівнювати знаменнику? Так, може! Наприклад, поділили прямоткуник на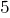 
рівних частин, і всі розфарбували. Отже, зафарбованих вийшло 
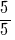прямокутника, що дорівнює 
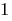, або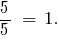 
Означення: Якщо у звичайному дробі чисельник менший від знаменника то дріб називається правильним дробом.
Означення: Якщо у звичайному дробі чисельник більший від знаменника то дріб називається неправильним дробом.
Дроби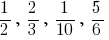 
— правильні дроби.
Дроби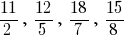 
— неправильні дроби.
Порівняння дробів
З двох дробів з однаковим знаменниками більший той, у кого чисельник більший.
Наприклад,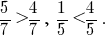 
Також, 
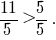Тому
Всі правильні дроби менші від одиниці, а неправильні — більші або дорівнюють одиниці. Кожний непавильний дріб більший за правильний!
Мішаний дріб. Мішане число
Неправильні дроби подають у вигляді мішаних чисел. Будь-який неправильний дріб можна представити в вигляді натурального числа або суми натурального числа і правильного дробу.
Число 
можна записати у вигляді суми двох дробів, наприклад, так: 
.
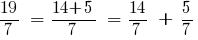Оскільки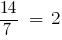 
, то 
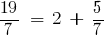
Суму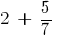 
прийнято записувати більш коротко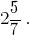 
Число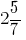 
називають мішаним числом. При цьому натуральне число 2 називають цілою частиною дробу, а правильний дріб 
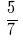— дробовою частиною дробу.
Означення: Мішаним числом називається число, яке записано в вигляді цілого числа і правильного дробу і розуміється, як сума цього числа і дробу.
Як перетворити неправильний дріб у мішане число
Щоб неправильний дріб перетворити в мішане число, у якого чисельник націло не ділиться на знаменник, треба чисельник поділити на знаменнник. Отримана неповна частка буде цілою частиною мішаного числа, а остача - чисельником його дробової частини.
Приклад: Перетворіть неправильний дріб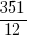 
у мішане число.
Розв'язування:
Поділимо чисельник дробу на знаменник. Вийшло: 29 - ціла частина числа, а остача дорівнює 3. Отже,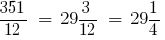 
Як перетворити мішане число у неправильний дріб
Щоб мішане число перетворити в неправильний дріб, треба цілу частину помножити на знаменнник дробової частини і до отриманого добуткудодати чисельник дробової частини. Отримана сума є чисельником неправильного дробу, а його знаменник дорівнює знаменнику дробової частини мішаного числа.
Приклад: Перетворіть мішане число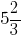 
у неправильний дріб.
Розв'язування:
Перетворюємо: 
Але Ви не хвилюйтесь, в найближчому часі cubens.com розробитиь калькулятори, які будуть допомагати Вам розв'язувати.