Поняття оберненої функції: Нехай функція  приймає кожне своє значення в єдиній точці її області визначення (така функція називається оборотною ). Тоді для кожного числа
приймає кожне своє значення в єдиній точці її області визначення (така функція називається оборотною ). Тоді для кожного числа  ( з множини значень функції
( з множини значень функції  ) існує єдине значення
) існує єдине значення  (з області визначення функції
(з області визначення функції  ), таке, що,
), таке, що, 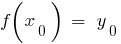 . Розглянемо нову функцію
. Розглянемо нову функцію 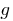 , яка кожному числу
, яка кожному числу  ставить у відповідність число
ставить у відповідність число  , тобто
, тобто 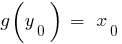 . У цьому випадку функція
. У цьому випадку функція 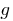 називається оберненою до функції
називається оберненою до функції  .
.
Властивості оберненої функції
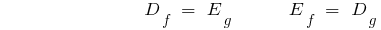
- Область визначення прямої функції є множиною значень оберненої, а множина значень прямої функції - область визначення оберненої.
- Якщо функція зростає (спадає) на деякому інтервалі, то вона має обернену функцію на цьому інтервалі, яка зростає, якщо пряма функція зростає, і спадає, якщо пряма функція спадає.
- Графіки прямої і оберненої функції симетричні відносно прямої
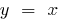 (бісектриси першого і третього координатних кутів)
(бісектриси першого і третього координатних кутів)
Приклади обернених функцій
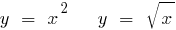
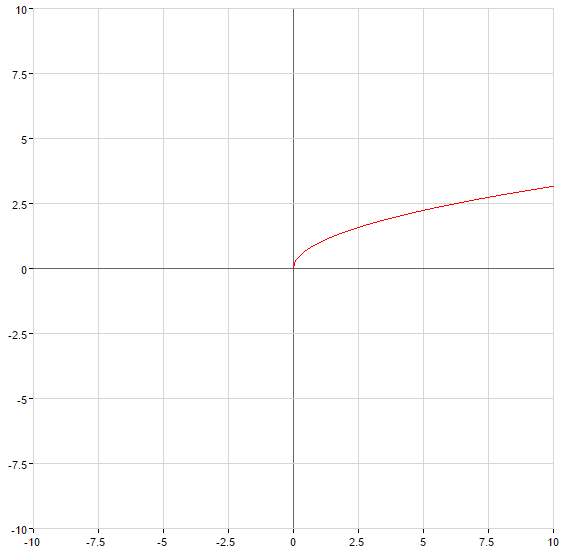
Приклад знаходження оберненої функції
Приклад: Знайти обернену функцію для функції: 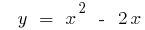
Розвязування: Знайдемо де задана функція зростає і спадає, 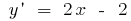 . Тоді
. Тоді 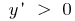 при
при 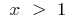 - функція зростає і
- функція зростає і 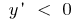 при
при 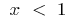 - функція спадає.
- функція спадає.
На кожному з цих проміжків 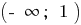 і
і 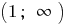 запишемо формулу оберненої функції. Оскільки
запишемо формулу оберненої функції. Оскільки 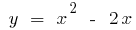 , то
, то 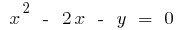 .
.
Звідси 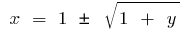 , тобто при
, тобто при 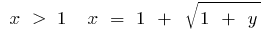 , а при
, а при 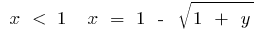 . Змінюючи позначення на традиційне, дістаємо: для функції
. Змінюючи позначення на традиційне, дістаємо: для функції 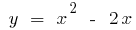 при
при 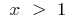 оберненою функцією буде функція
оберненою функцією буде функція 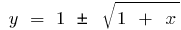 , а при
, а при 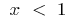 оберненою функцією буде функція
оберненою функцією буде функція 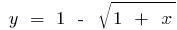 .
.

 (бісектриси першого і третього координатних кутів)
(бісектриси першого і третього координатних кутів)