O conceito de função de feedback: Deixe a função  toma cada um o seu valor em um único ponto de sua definição de área (uma função chamada reversível ). Então, para cada número
toma cada um o seu valor em um único ponto de sua definição de área (uma função chamada reversível ). Então, para cada número  ( a partir do conjunto de valores da função
( a partir do conjunto de valores da função  ) existe um único valor
) existe um único valor  (a partir do painel de definição de função
(a partir do painel de definição de função  ), de tal forma que,
), de tal forma que, 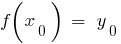 . Considere uma nova função
. Considere uma nova função 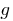 que associa a cada número
que associa a cada número  o coloca em conformidade com o número
o coloca em conformidade com o número  , ou seja,
, ou seja, 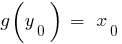 . Nesse caso, o recurso
. Nesse caso, o recurso 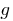 é chamado de feedback para a função
é chamado de feedback para a função  .
.
Propriedades da função inversa
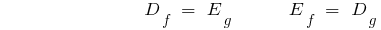
- A área de detecção direta de uma função é um conjunto de valores de feedback, e um conjunto de valores direto de recursos - área de detecção de feedback.
- Se a função é crescente (decrescente) em um determinado intervalo, ela tem a função inversa neste intervalo, que cresce, se a função direta aumenta, e diminui se a função direta vem.
- Gráficos direta e inversa de uma função simétrica relativamente simples
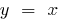 (биссектрисы primeiro e terceiro eixos de ângulos)
(биссектрисы primeiro e terceiro eixos de ângulos)
Exemplos de funções inversas
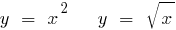
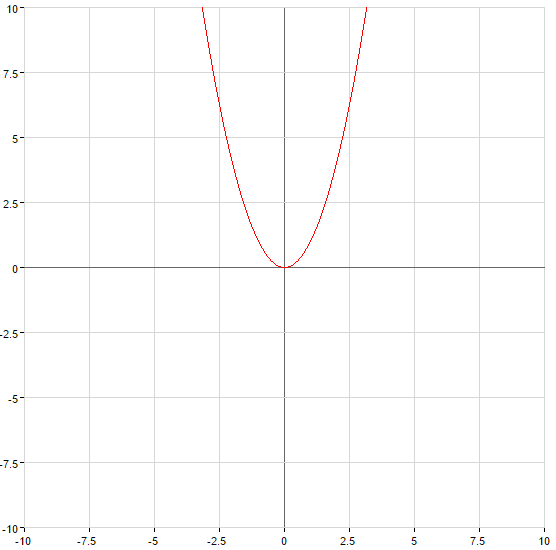
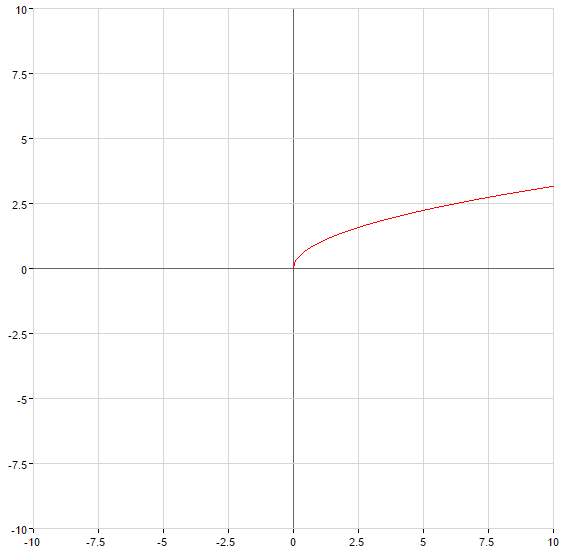
Exemplo de funções inversas
Exemplo: Encontrar a inversa de uma função para a função de: 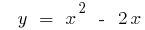
Solução: Encontrar onde a função especificada aumenta e diminui, 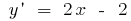 . Então,
. Então, 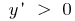 quando
quando 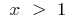 a função aumenta
a função aumenta 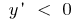 quando a
quando a 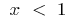 função é decrescente.
função é decrescente.
Em cada um destes períodos 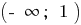 e
e 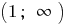 vou escrever a fórmula da inversa de uma função. Pois
vou escrever a fórmula da inversa de uma função. Pois 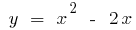 , então
, então 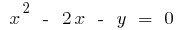 .
.
A partir daqui 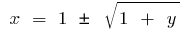 , ou seja, quando
, ou seja, quando 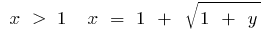 , em quando
, em quando 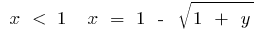 . Alterando a designação tradicional, temos: para a função
. Alterando a designação tradicional, temos: para a função 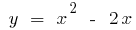 quando
quando 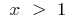 a função inversa da função
a função inversa da função 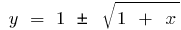 , quando
, quando 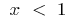 a função inversa da função
a função inversa da função 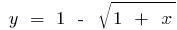 .
.

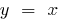 (биссектрисы primeiro e terceiro eixos de ângulos)
(биссектрисы primeiro e terceiro eixos de ângulos)