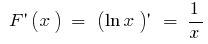Original
Definição:uma Função 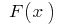 é chamada inicial para a função
é chamada inicial para a função  neste intervalo se para quaisquer
neste intervalo se para quaisquer  a partir deste período
a partir deste período 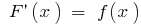
Exemplos
- Para a função
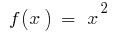 no intervalo
no intervalo 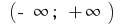 inicial é a
inicial é a 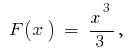 vez
vez 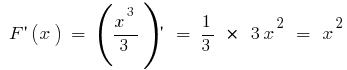
- Para a função
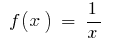 no intervalo
no intervalo 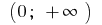 inicial é a
inicial é a 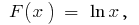 vez
vez 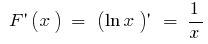
A principal propriedade de integrais
Se a função 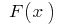 é o inicial para a função
é o inicial para a função  neste intervalo, e
neste intervalo, e 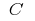 — uma constante, então a função
— uma constante, então a função 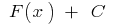 também é o inicial para a função
também é o inicial para a função 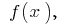 neste caso, qualquer первообразная para a função
neste caso, qualquer первообразная para a função  neste intervalo, pode ser escrita como
neste intervalo, pode ser escrita como 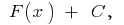 onde
onde 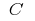 — tornou-se uma
— tornou-se uma
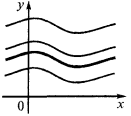
Sentido geométrico
Gráficos de qualquer integrais esta função são obtidos fora de si paralela de transferência ao longo do eixo 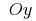
A integral indefinida
Definição:o Conjunto de todas as integrais esta função  é chamada incerto интегралом e indicado por um símbolo de
é chamada incerto интегралом e indicado por um símbolo de 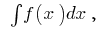 т. е.
т. е. 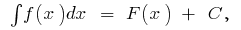 onde
onde 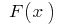 um dos integrais de funções
um dos integrais de funções 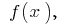 e
e 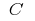 uma certa tornou-se
uma certa tornou-se
Regras de integração
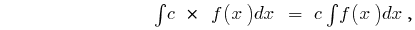 onde
onde 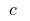 tornou — se o
tornou — se o
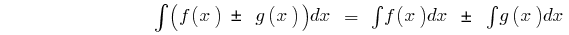
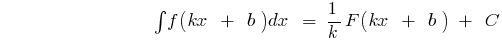

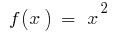 no intervalo
no intervalo 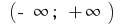 inicial é a
inicial é a 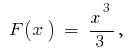 vez
vez 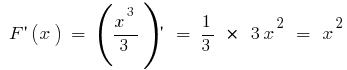
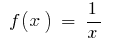 no intervalo
no intervalo 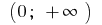 inicial é a
inicial é a 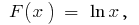 vez
vez