Definição: Показниково-степенное equação  — a equação que contém uma expressão de tipo
— a equação que contém uma expressão de tipo 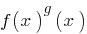 , ou seja, a equação do tipo
, ou seja, a equação do tipo 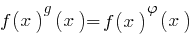
As principais formas de resolver показниково-степенных equações e inequações
 Para o caso de f(x)>0
Para o caso de f(x)>0
Exemplo 1
Solução:
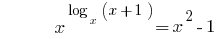
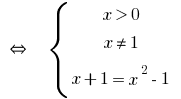
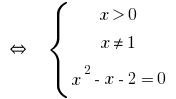
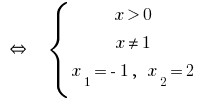
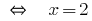
Resposta: 
Exemplo 2
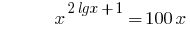
Solução:
No ОДЗ  ambas as partes da equação são positivos, então depois de логарифмирования base 10, obtemos a equação равносильное este
ambas as partes da equação são positivos, então depois de логарифмирования base 10, obtemos a equação равносильное este 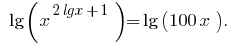
A partir daqui 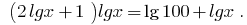
Substituição 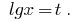
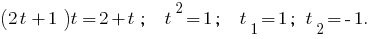
Então, 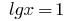 ou
ou 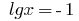 , т. е.
, т. е. 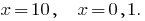 (ambos de raiz conduzem à ОДЗ)
(ambos de raiz conduzem à ОДЗ)
Resposta: 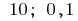
 Para o caso de f(x) — aleatória de expressão
Para o caso de f(x) — aleatória de expressão
Exemplo 3
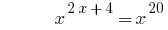
Solução:
Se considerada a base do  número
número
1) quando o 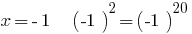 correto igualdade;
correto igualdade;
2) quando 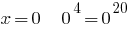 corretamente;
corretamente;
3) quando 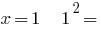 corretamente;
corretamente;
4) quando 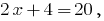 então há uma
então há uma 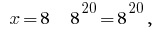 certa igualdade.
certa igualdade.
Resposta: 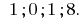
Nota: Se considerar a base  de uma variável, então a função
de uma variável, então a função 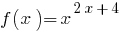 é considerada incorrida apenas quando
é considerada incorrida apenas quando 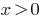 . Deste ponto de vista, esta equação só vai ter duas raízes:
. Deste ponto de vista, esta equação só vai ter duas raízes: 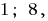

 Para o caso de f(x)>0
Para o caso de f(x)>0