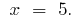Solução de equações através de equações-efeito
- A conversão, garantir a conservação correta de igualdade
- Verificação de raízes em substituição a equação original
Solução de equações utilizando равносильных transformação
- Considerar ОДЗ correta a igualdade e referencias de transformação
- Salvar no ОДЗ correta a igualdade e referencias de transformação
Solução de equações. Substituição de variáveis
Se na equação a variável faz da mesma forma, é conveniente a expressão variável, designado por uma letra do alfabeto (nova variável).
Exemplo 1.
Розвяжіть equação: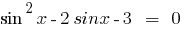 
Розвязання.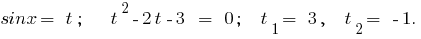 
1. Quando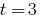 
a equação 
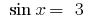de raízes não tem, porque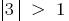 
2. Quando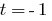 
temos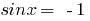 
, então,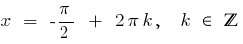 
Resposta: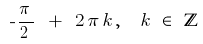
Exemplo 2.
Розвяжіть equação: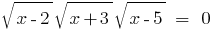 
Розвязання. Pois, sob o signo da raiz парного степеня pode estar apenas невідємні de expressão, então o intervalo de valores permitidos (ОДЗ) de um determinado equação define o sistema de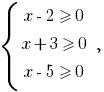 
розвязком que é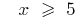 
A obra é igual a zero se, e somente então, quando um dos factores primos é igual a zero, e todos os outros multiplicadores existem: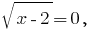 
quando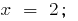 
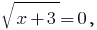quando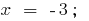 
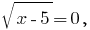quando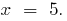 
O valor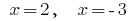 
não está incluído no ОДЗ especificado equação, portanto, eles não são raízes de um determinado equação.
O valor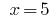 
está incluído na ОДЗ, então, 
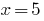é a raiz de um determinado equação.
Resposta: