समीकरण को हल करने का उपयोग कर समीकरण और प्रभाव
- रूपांतरण के संरक्षण की गारंटी का अधिकार समानता के
- जाँच जड़ों प्रतिस्थापन द्वारा मूल समीकरण में
समीकरणों को हल करके बराबर परिवर्तनों का उपयोग कर
- नोट आईडी के बराबर के लिए दोनों आगे और रिवर्स परिवर्तनों
- पर बचाने के लिए सरकारी विभाग के लिए बराबर दोनों आगे और रिवर्स परिवर्तनों
समाधान के समीकरण है. परिवर्तन के चर
यदि समीकरण में चर होता है एक ही रूप में चाहे, इसी अभिव्यक्ति के साथ एक चर को चिह्नित करने के लिए एक पत्र (एक नया चर).
उदाहरण 1.
Rozwarte समीकरण: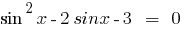 
Rozwiazania.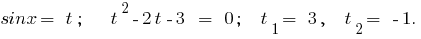 
1. यदि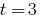 
समीकरण में 
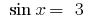कोई जड़ों की है क्योंकि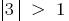 
2. यदि आप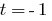 
है 
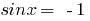, तो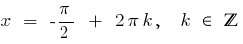 
जवाब: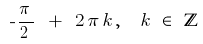
उदाहरण 2.
Rozwarte समीकरण: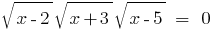 
Rozwiazania. क्योंकि रूट के अंतर्गत साइन जोड़ी रूपों में अकेले खड़े हो सकते हैं newmn अभिव्यक्ति है, तो इस क्षेत्र की स्वीकार्य मूल्यों (आईडीएस) के दिए गए समीकरण द्वारा दिया जाता है एक प्रणाली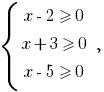 
rozvyazka है जो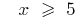 
उत्पाद शून्य के बराबर है यदि और केवल यदि एक मल्टीप्लायरों के बराबर शून्य करने के लिए, और अन्य सभी मल्टीप्लायरों मौजूद: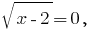 
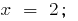
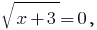जब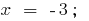 
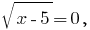जब 
जब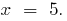 
मूल्य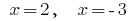 
में शामिल नहीं है odz के समीकरण है, इसलिए, वे नहीं कर रहे हैं जड़ों के समीकरण है.
मूल्य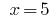 
में शामिल सरकारी विभाग, तो 
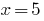एक रूट के समीकरण है.
जवाब: