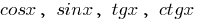वृद्धि और घटते कार्यों
के एक समारोह 
में वृद्धि
तो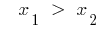 
, 
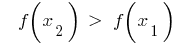
के लिए सभी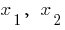 
का क्षेत्र परिभाषाओं (की वृद्धि के साथ बहस इसी ग्राफ के अंक आरोही उपजा)
समारोह के उतरते
तो ,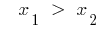 
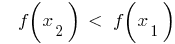
के लिए सभी 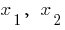का क्षेत्र परिभाषाओं (वृद्धि के साथ तर्क के इसी अंक के ग्राफ से छोड़े गए)
और भी अजीब कार्यों
समारोह भी
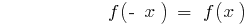
के लिए सभी 
का क्षेत्र परिभाषाएँ. का ग्राफ भी एक समारोह है करने के लिए सममित अक्ष vanocni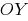 
एक समारोह में अजीब है
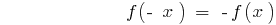
के लिए सभी का क्षेत्र परिभाषाएँ. ग्राफ की एक अजीब समारोह सममित है vanocni मूल के हैं.
आवृत्ति
परिभाषा: एक समारोह में कहा जाता है समय-समय के साथ अवधि 
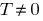के लिए यदि किसी का निर्धारण करने के समारोह में संख्या और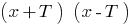 
भी करने के लिए संबंधित गुंजाइश है और वैधता के समीकरण
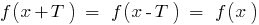है ।
अंतराल के माध्यम से लंबाई में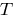 
ग्राफ का एक आवधिक समारोह में खुद को दोहराता है ।
अवधि सुविधाओं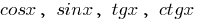 
कार्य करता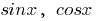 
है की अवधि 
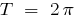है ।
कार्य करता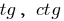 
है की अवधि 
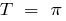है ।