परिभाषा:यदि एक समारोह  परिभाषित पर एक अंतराल
परिभाषित पर एक अंतराल  और
और 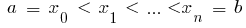 फिर एक निश्चित अभिन्न एक समारोह के
फिर एक निश्चित अभिन्न एक समारोह के  एक अंतराल पर
एक अंतराल पर  एक संख्या है बराबर करने के लिए सीमा के अभिन्न अंग योग
एक संख्या है बराबर करने के लिए सीमा के अभिन्न अंग योग 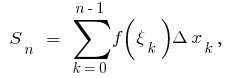 जहां
जहां 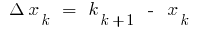 एफ
एफ 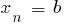
कि है
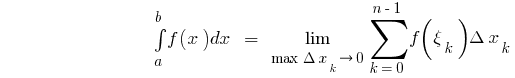
जहां 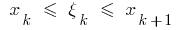 मैं
मैं 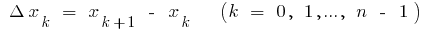
के निर्माण के अभिन्न रकम के लिए उदाहरण के क्षेत्र का निर्धारण करने के लिए वक्रीय चतुर्भुज
चलो खंड पर  सेट है करने के लिए एक अभिन्न और सतत समारोह
सेट है करने के लिए एक अभिन्न और सतत समारोह 
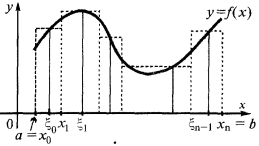
के क्षेत्र का निर्धारण करने के लिए वक्रीय चतुर्भुज (घिरा वक्र 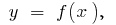 एक्सिस
एक्सिस 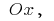 और सीधे,
और सीधे,  और
और 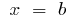 ), विभाजित काट
), विभाजित काट  अंक
अंक 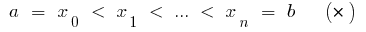
पर 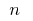 चयनित भागों में से प्रत्येक पर प्राप्त आंशिक क्षेत्रों
चयनित भागों में से प्रत्येक पर प्राप्त आंशिक क्षेत्रों 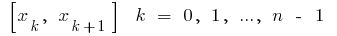 की एक मनमाने ढंग से बात के
की एक मनमाने ढंग से बात के 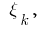 मूल्यों की गणना
मूल्यों की गणना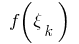 के समारोह के साथ
के समारोह के साथ  इन बिंदुओं पर और फार्म की राशि
इन बिंदुओं पर और फार्म की राशि 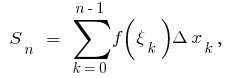 , जहां
, जहां 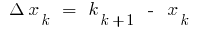
इस राशि के बराबर की राशि के क्षेत्रों छायांकित आयतों कहा जाता है अभिन्न योग है ।
अगर अब की संख्या से विभाजित अंक बढ़ जाती है अनिश्चित काल के लिए, और अधिकतम लंबाई (उच्चतम) आंशिक कटौती विभाजन शून्य करने के लिए जाता है, और मूल्य 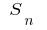 के लिए जाता है, एक निश्चित सीमा
के लिए जाता है, एक निश्चित सीमा  पर निर्भर नहीं करता है विधि के विभाजन
पर निर्भर नहीं करता है विधि के विभाजन 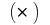 और विकल्प के अंक
और विकल्प के अंक 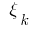 पर आंशिक खंडों, तो मूल्य
पर आंशिक खंडों, तो मूल्य 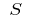 कहा जाता है के क्षेत्र वक्रीय चतुर्भुज, यानी
कहा जाता है के क्षेत्र वक्रीय चतुर्भुज, यानी 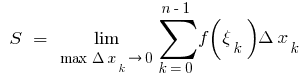
सूत्र न्यूटन लाइबनिट्स
यदि इस समारोह  परिभाषित किया है और निरंतर अंतराल पर
परिभाषित किया है और निरंतर अंतराल पर  और
और 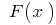 अपने अभिन्न (यानी
अपने अभिन्न (यानी 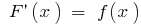 ) है, तो
) है, तो 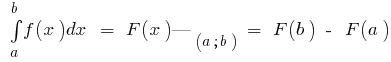
उदाहरण है । के रूप में 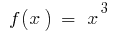 एक आदिम
एक आदिम 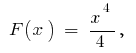 तो
तो 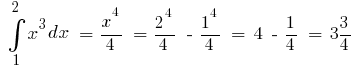
के बुनियादी गुणों को निश्चित अभिन्न
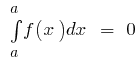
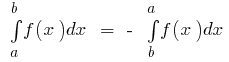
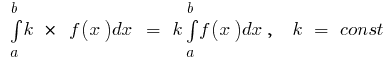
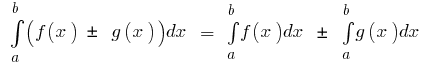
- यदि
 एकीकृत पर
एकीकृत पर  और
और 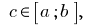 फिर
फिर
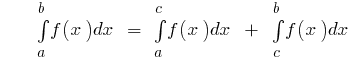

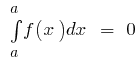
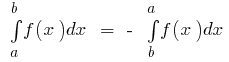
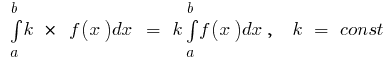
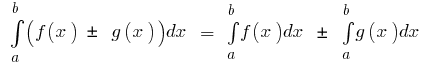
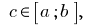 फिर
फिर