Definición:Si la función 
está definida en el intervalo 
y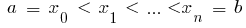 
, de cierta integrada de la función en el intervalo se llama un número igual de límite de la integral de la suma de 
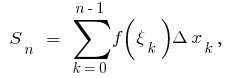donde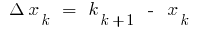 
, f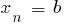 
es decir,
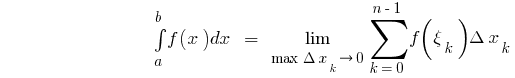
donde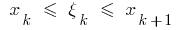 
i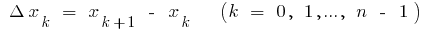 
La construcción integral de la suma en el ejemplo de la definición de la plaza de la curva de corte a
Que en el tramo de la se establece неотъемлемою y continua de la función
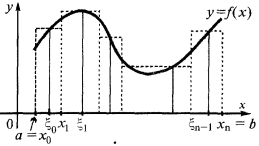
Para determinar el tamaño de la curva de un trapecio (una curva limitada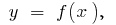 
por el eje 
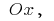y directos, 
y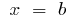 
), de dividir el segmento de los puntos de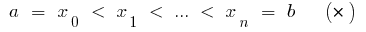 
en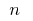 
partes, escogemos en cada uno de los parciales de los trozos de 
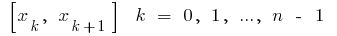un punto arbitrario 
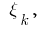se calcula el valor
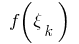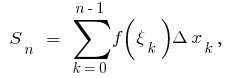de la función en estos puntos, y componemos la suma de donde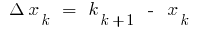
Esta cantidad es igual a la suma de las superficies de заштрихованных rectángulos y se llama la integral de la suma.
Si ahora el número de puntos de ruptura indefinidamente, aumenta la longitud máxima (mayor) parcial del corte de la ruptura tiende a cero, y cuando este valor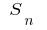 
tiende a un límite determinado 
no depende de la forma de la ruptura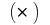 
y la selección de puntos 
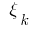en el parcial de dichos segmentos, el valor 
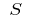se llama la plaza de la curva de trapecio, es decir,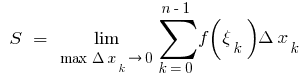 
La Fórmula De Newton - Leibniz
Si la función está definida y es continua en el intervalo y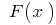 
su первообразная (es decir, 
), 
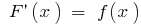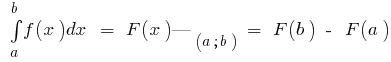
Ejemplo. Dado que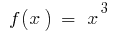 
una de las primitivas de 
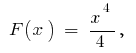lo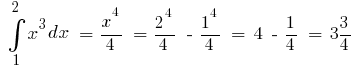 
Las principales propiedades de un determinado desarrollo integral
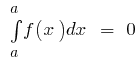
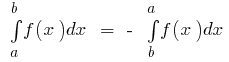
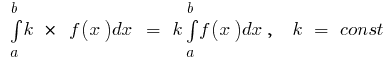
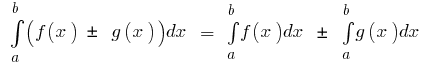
- Si
integrado en el 
y 
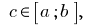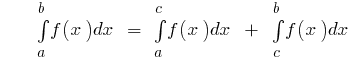
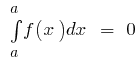
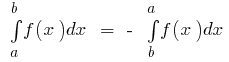
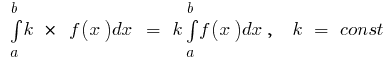
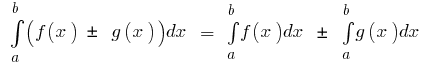
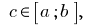lo
lo