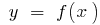Ejemplo. 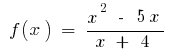
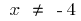
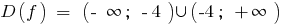
La función ni par ni impar y periódica
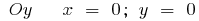
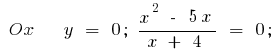
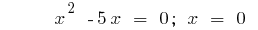 o
o 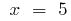
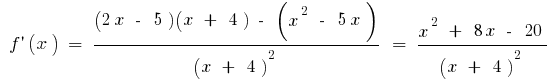
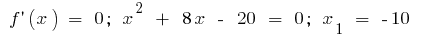 o
o 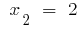
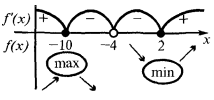
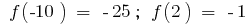
Encontrar los puntos de inflexión (si existen) y los valores  en los puntos de inflexión de la
en los puntos de inflexión de la
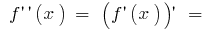
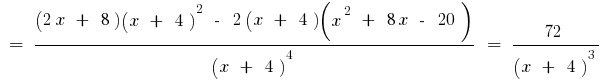
Así 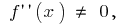 es el signo de la segunda derivada puede variar sólo en el punto de
es el signo de la segunda derivada puede variar sólo en el punto de 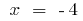
- La definición del área
- La paridad, paridad impar, la periodicidad de la
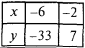
- Intersección con los ejes de coordenadas
- Derivada y puntos críticos de
- Intervalos ascendente, descendente y el punto extremo (y los valores de la función en estos puntos)
- El comportamiento de la función en los extremos del dominio y las asíntotas gráfica de la función (verticales, horizontales y oblicuas)
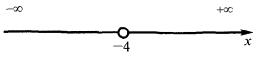
Al
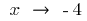 de la izquierda
de la izquierda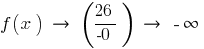
Cuando
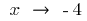 el asunto
el asunto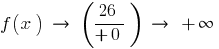
Por lo tanto,
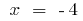 es asíntota vertical
es asíntota verticalPorque
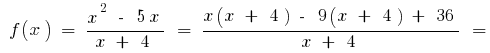
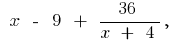 cuando
cuando 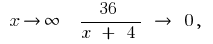 entonces,
entonces, 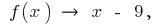 es decir,
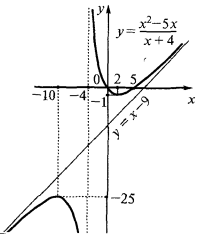
es decir, 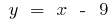 es asíntota oblicua
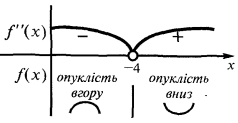
es asíntota oblicua - La segunda derivada y la investigación de la función en el bulto y угнутість
- Si desea encontrar los puntos de control que mejoran el comportamiento de la gráfica
- En base a la investigación realizada, construyendo una miniatura de la gráfica de la función
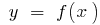


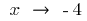 de la izquierda
de la izquierda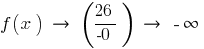
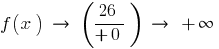
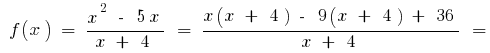
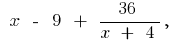 cuando
cuando 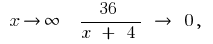 entonces,
entonces, 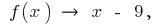 es decir,
es decir, 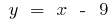 es asíntota oblicua
es asíntota oblicua