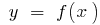উদাহরণ. 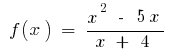
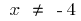
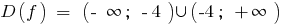
ফাংশন হয় না, এমনকি বা বিজোড় এবং পর্যায়ক্রমিক
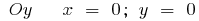
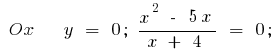
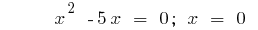 বা
বা 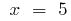
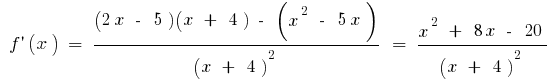
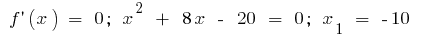 বা
বা 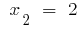
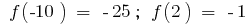
এটি আনতি পয়েন্ট (যদি তাদের অস্তিত্ব) এবং মান  মধ্যে পয়েন্ট আনতি
মধ্যে পয়েন্ট আনতি
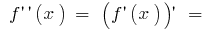
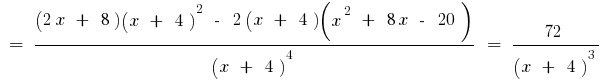
তাই 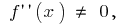 সাইন এর দ্বিতীয় ডেরিভেটিভ পরিবর্তন করতে পারেন শুধুমাত্র সময়ে
সাইন এর দ্বিতীয় ডেরিভেটিভ পরিবর্তন করতে পারেন শুধুমাত্র সময়ে 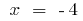
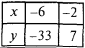
- সুযোগ
- প্যারিটি বিজোড় প্যারিটি, পর্যাবৃত্তি
- ছেদ সঙ্গে তুল্য অক্ষ
- ডেরিভেটিভ এবং সমালোচনামূলক পয়েন্ট
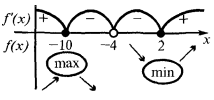
- অন্তর বৃদ্ধি, হ্রাস এবং চরম পয়েন্ট (এবং মান ফাংশন এ এই পয়েন্ট)
- আচরণ ফাংশন এর শেষ এ, সুযোগ ও করে, asymptotes এর একটি ফাংশনের গ্রাফ (উল্লম্ব, অনুভূমিক এবং আনত)
যখন আপনি
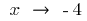 বাম
বাম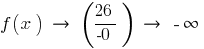
এ
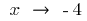 ক্ষেত্রে
ক্ষেত্রে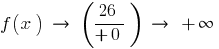
অতএব
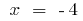 — উল্লম্ব asymptote
— উল্লম্ব asymptoteযেহেতু
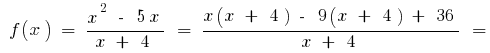
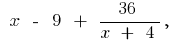 যখন
যখন 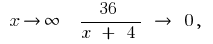 তখন
তখন 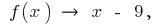 ইন্টারনেট
ইন্টারনেট 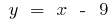 - এ তেরছা asymptote
- এ তেরছা asymptote - দ্বিতীয় ডেরিভেটিভ এবং গবেষণা of the function of the bulge এবং gnutt
- যদি আপনি এটি করতে চান নিয়ন্ত্রণ পয়েন্ট উল্লেখ আচরণ গ্রাফ
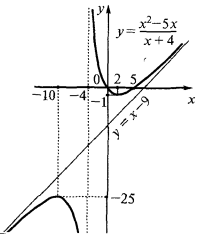
- এর ভিত্তিতে গবেষণা বিল্ডিং স্কেচ গ্রাফ এর একটি ফাংশন
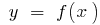


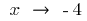 বাম
বাম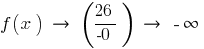
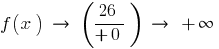
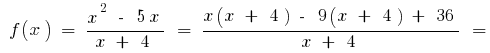
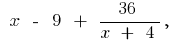 যখন
যখন 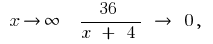 তখন
তখন 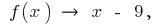 ইন্টারনেট
ইন্টারনেট 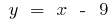 - এ তেরছা asymptote
- এ তেরছা asymptote