সংজ্ঞা: এর ফাংশন ফর্ম 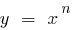 যেখানে n হচ্ছে যেকোন বাস্তব সংখ্যা বলা হয়, ক্ষমতা ফাংশন
যেখানে n হচ্ছে যেকোন বাস্তব সংখ্যা বলা হয়, ক্ষমতা ফাংশন
বৈশিষ্ট্য, ক্ষমতা ফাংশন ( 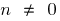 )
)
a) n — প্রাকৃতিক  b) n একটি পূর্ণসংখ্যা WMA
b) n একটি পূর্ণসংখ্যা WMA  গ) n নয়, একটি পুরো
গ) n নয়, একটি পুরো
একটি)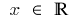
বি)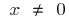
গ) যখন 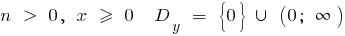
 যখন
যখন 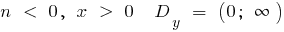
ক) যখন বৃদ্ধ ও টেনিস 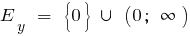
 যখন n বিজোড় হয়
যখন n বিজোড় হয় 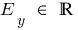
খ) যখন বৃদ্ধ ও টেনিস 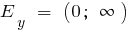
 যখন n বিজোড় হয়
যখন n বিজোড় হয় 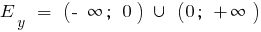
গ) যখন 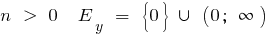
 যখন
যখন 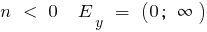
a),b) যখন বৃদ্ধ ও টেনিস — টেনিস
 যখন n - বিজোড় — বিজোড়
যখন n - বিজোড় — বিজোড়
গ) কেউই, এমনকি বা বিজোড়
না, পর্যায়
একটি) 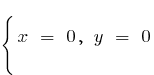
খ) কোন
গ) যখন 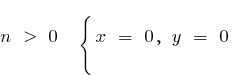
 যখন
যখন  — কোন
— কোন
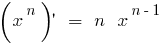
ক) যখন বৃদ্ধ ও টেনিস 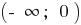 — কমে,
— কমে,  বাড়ে
বাড়ে
 যখন n বিজোড় — বাড়ছে
যখন n বিজোড় — বাড়ছে
খ) যখন বৃদ্ধ ও টেনিস 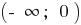 — বাড়ে
— বাড়ে  — কমে যায়
— কমে যায়
 যখন n বিজোড়
যখন n বিজোড় 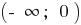 — আসে
— আসে  — আসে
— আসে
গ) যখন 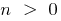 বর্ধমান
বর্ধমান
 যখন এটা
যখন এটা  আসে
আসে
ক) যখন বৃদ্ধ ও টেনিস 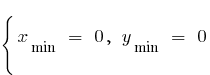
 যখন n - বিজোড় — কোন
যখন n - বিজোড় — কোন
খ) কোন
গ) যখন 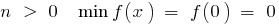
 যখন
যখন 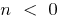 — কোন
— কোন
ক) কোন
বি) 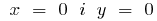
গ) করেননি 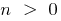 — না
— না
 যখন
যখন 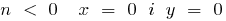
ক) যখন বৃদ্ধ ও টেনিস  — স্ফীতি নিচে
— স্ফীতি নিচে
 যখন n বিজোড় হয়,
যখন n বিজোড় হয়, 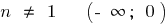 —
— 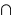 ;
;  —
—  ; 0 — আনতি বিন্দু
; 0 — আনতি বিন্দু
খ) যখন বৃদ্ধ ও টেনিস — 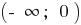 —
—  ;
;  —
— 
 যখন n - বিজোড় —
যখন n - বিজোড় — 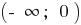 —
— 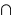 ;
;  —
— 
গ) যখন 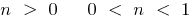 —
— 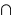 ;
; 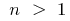 —
— 
 যখন
যখন 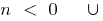
তাহলে 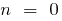 ,
, 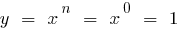 (যখন
(যখন 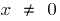 )
)
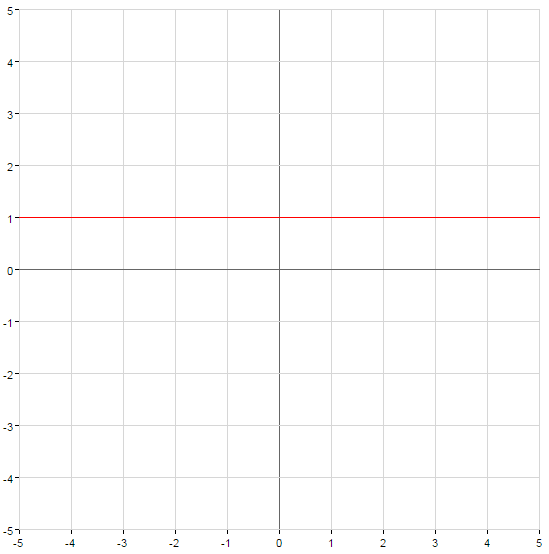
- সুযোগ

- একাধিক মান

- প্যারিটি বিজোড় প্যারিটি
- ফ্রিকোয়েন্সি
- ছেদ সঙ্গে তুল্য অক্ষ
- ডেরিভেটিভ
- বৃদ্ধি এবং হ্রাস
- Extrema
- Asymptotes
- Convexity এবং আনতি পয়েন্ট
- একটি বিশেষ ক্ষেত্রে
গ্রাফ ক্ষমতার ফাংশন

- n একটি এমনকি প্রাকৃতিক সংখ্যা
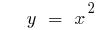
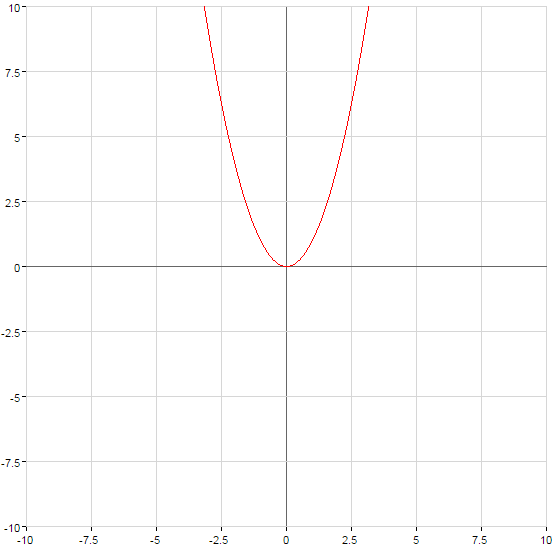
- n — একটি অদ্ভুত প্রাকৃতিক সংখ্যা
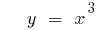
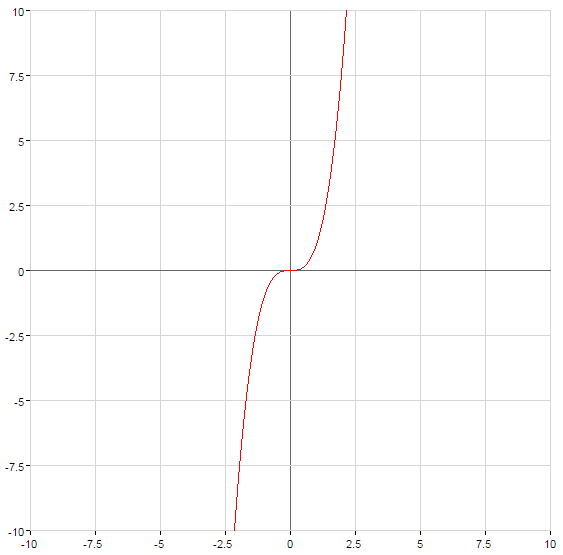
- n একটি বিজোড় সংখ্যা VDA
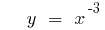
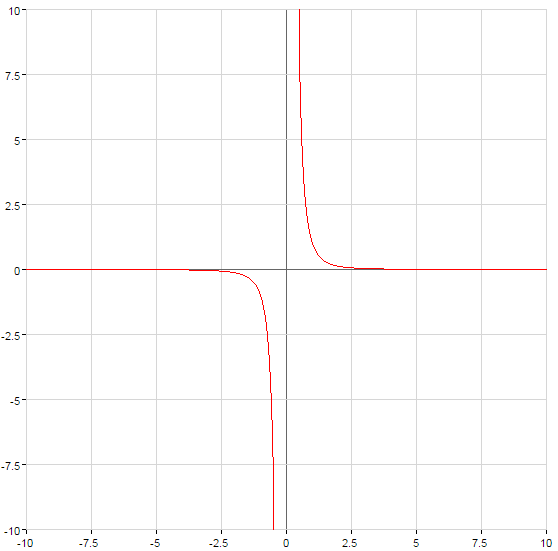
- n একটি জোড় সংখ্যা VDA
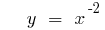
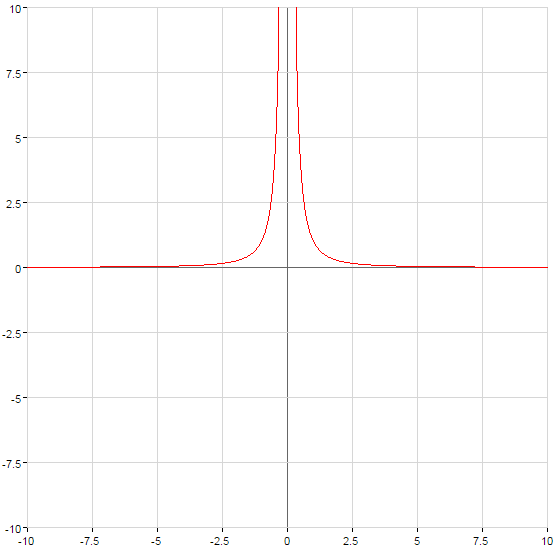
- n নয়, ইতিবাচক পূর্ণসংখ্যা
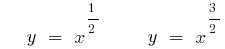 (সবুজ)
(সবুজ)
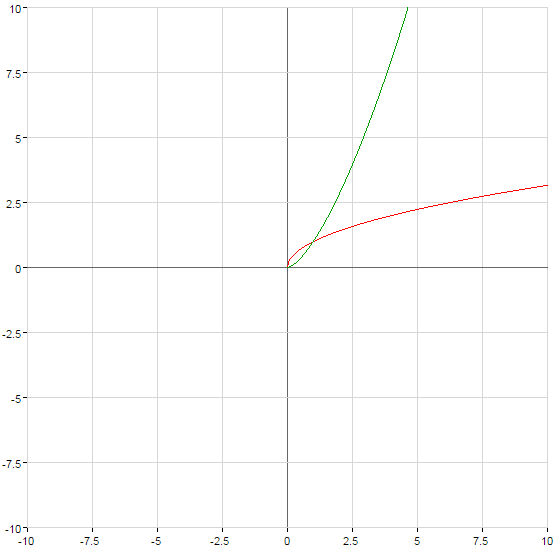
- n একটি পূর্ণসংখ্যা না হয়, WMA
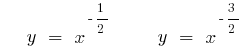 (সবুজ)
(সবুজ)
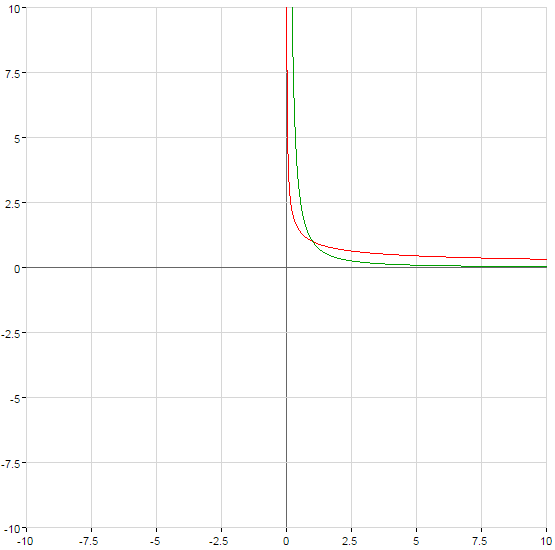

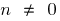 )
)
