গতানুগতিকতা এবং ধারাবাহিকতা ফাংশন
একটি যথেষ্ট শর্ত বৃদ্ধি জন্য ফাংশন
যদি প্রতিটি সময়ে ব্যবধান 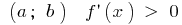 ফাংশন বাড়ছে এই ব্যবধান
ফাংশন বাড়ছে এই ব্যবধান
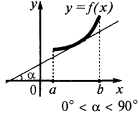
একটি যথেষ্ট শর্ত কমে জন্য ফাংশন
যদি প্রতিটি সময়ে ব্যবধান 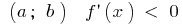 ফাংশন হ্রাস করা হয় এই ব্যবধান
ফাংশন হ্রাস করা হয় এই ব্যবধান
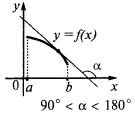
মন্তব্য. এই অবস্থার শুধুমাত্র যথেষ্ট, কিন্তু না জন্য প্রয়োজনীয় শর্ত বৃদ্ধি এবং হ্রাস ফাংশন
একটি প্রয়োজনীয় এবং যথেষ্ট শর্ত দৃঢ়তা ফাংশন
একটি ফাংশন,  ধ্রুবক একটি ব্যবধান
ধ্রুবক একটি ব্যবধান 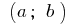 যদি এবং কেবল যদি, যখন
যদি এবং কেবল যদি, যখন  সব পয়েন্ট ব্যবধান
সব পয়েন্ট ব্যবধান
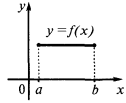
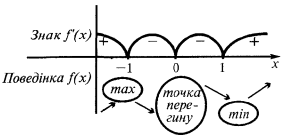
এই চরম (maximums এবং নূন্যতম) ফাংশন
সর্বোচ্চ পয়েন্ট
সংজ্ঞা: যে পয়েন্ট  অফ সংজ্ঞা ফাংশন
অফ সংজ্ঞা ফাংশন  বলা হয়, সর্বোচ্চ বিন্দু , এই ফাংশন আছে, তাহলে
বলা হয়, সর্বোচ্চ বিন্দু , এই ফাংশন আছে, তাহলে 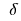 একটি আশপাশ
একটি আশপাশ 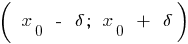 বিন্দু
বিন্দু  যে সব জন্য
যে সব জন্য 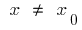 এই আশপাশ থেকে বৈষম্য
এই আশপাশ থেকে বৈষম্য 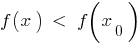
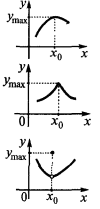
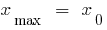 — সর্বোচ্চ পয়েন্ট
— সর্বোচ্চ পয়েন্ট
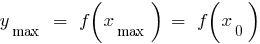 — সর্বোচ্চ
— সর্বোচ্চ
বিন্দু একটি সর্বনিম্ন
সংজ্ঞা: যে পয়েন্ট  অফ সংজ্ঞা ফাংশন
অফ সংজ্ঞা ফাংশন  বলা হয়, সর্বনিম্ন বিন্দু এই ফাংশন আছে, তাহলে
বলা হয়, সর্বনিম্ন বিন্দু এই ফাংশন আছে, তাহলে 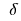 একটি আশপাশ
একটি আশপাশ 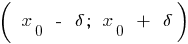 বিন্দু
বিন্দু  যে সব জন্য
যে সব জন্য 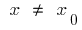 এই আশপাশ থেকে বৈষম্য
এই আশপাশ থেকে বৈষম্য 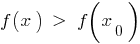
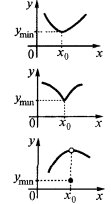
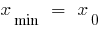 — সর্বনিম্ন পয়েন্ট
— সর্বনিম্ন পয়েন্ট
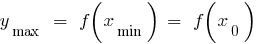 — সর্বনিম্ন
— সর্বনিম্ন
সন্ধিক্ষনে
সংজ্ঞা: স্বরাষ্ট্র পয়েন্ট ডোমেইন এর সংজ্ঞা ফাংশন যেখানে ব্যুৎপন্ন হয় শূন্য বা অস্তিত্ব নেই বলা হয়, সমালোচনামূলক
প্রয়োজনীয় শর্ত জন্য একটি extremum
 — extremum পয়েন্ট
— extremum পয়েন্ট 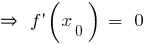 বা
বা 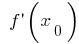 না বিদ্যমান
না বিদ্যমান
(কিন্তু না প্রতিটি বিন্দুতে  যেখানে
যেখানে 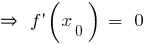 বা
বা 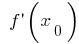 না হতে হবে, একটি extremum!)
না হতে হবে, একটি extremum!)
যথেষ্ট শর্ত extremum
এ বিন্দু  চিহ্ন
চিহ্ন 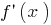 পরিবর্তন
পরিবর্তন 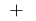 এ
এ 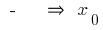 বিন্দু সর্বোচ্চ
বিন্দু সর্বোচ্চ
এ বিন্দু  চিহ্ন
চিহ্ন 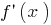 পরিবর্তন
পরিবর্তন 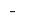 এ
এ 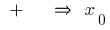 বিন্দু সর্বনিম্ন
বিন্দু সর্বনিম্ন
একটি উদাহরণ একটি গ্রাফ এর একটি ফাংশন  আছে যে একটি extremum
আছে যে একটি extremum
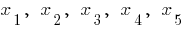 — সন্ধিক্ষনে
— সন্ধিক্ষনে
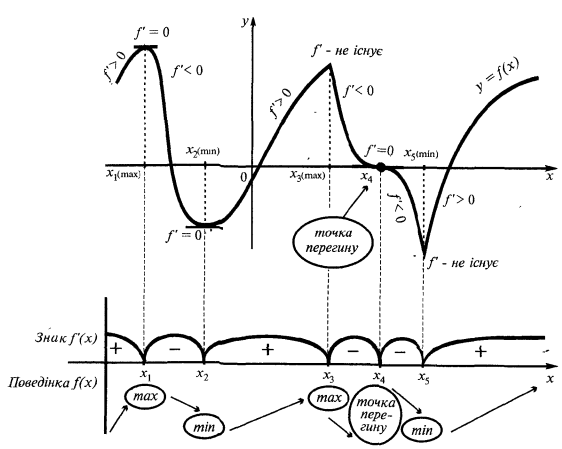
অধ্যয়নের উপর ফাংশন monotonicity এবং extrema
উদাহরণ. 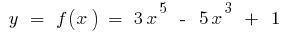
সুযোগ: 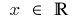
ফাংশন হয়, ক্রমাগত প্রতিটি বিন্দু তার ডোমেইন এর সংজ্ঞা
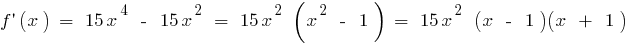
 সেখানে সমগ্র সুযোগ
সেখানে সমগ্র সুযোগ
 যখন
যখন 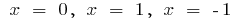
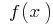 সঙ্গে বৃদ্ধি পায়,
সঙ্গে বৃদ্ধি পায়, 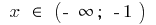 এবং
এবং 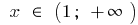
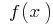 ভর্তুকিও যখন
ভর্তুকিও যখন 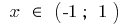
চরম পয়েন্ট: 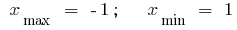
চরম: 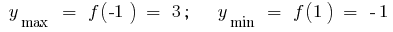
- এটি ডোমেইন এর সংজ্ঞা এবং অন্তর যা ফাংশন ক্রমাগত
- খুঁজে বের করতে ডেরিভেটিভ

- এটি সমালোচনামূলক পয়েন্ট, অর্থাৎ প্রত্যন্ত পয়েন্ট যেখানে নির্ণয়
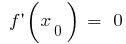 বা না আছে
বা না আছে - বোঝান, সমালোচনামূলক বিন্দু ডোমেইন এর সংজ্ঞা খুঁজে লক্ষণ ব্যুৎপন্ন এবং প্রকৃতি ফাংশন প্রতিটি ব্যবধান, যা splits সংজ্ঞা এলাকায়
- প্রতিটি গুরুত্বপূর্ণ পয়েন্ট নির্ধারণ কিনা, এটা উচ্চ বা নিম্ন বা না হয় একটি extremum পয়েন্ট
- রেকর্ড porni ফলাফল অধ্যয়ন (অন্তর এর monotonicity এবং extrema)
সর্বোচ্চ এবং সর্বনিম্ন মান ক্রমাগত ফাংশন ব্যবধান
সম্পত্তি: যদি ফাংশন হয়,  ক্রমাগত একটি ব্যবধান আছে এবং তাতে একটি সসীম সংখ্যা সমালোচনামূলক পয়েন্ট, তারপর, এটা attains তার সর্বোচ্চ এবং সর্বনিম্ন মান উপর এই ব্যবধান হয় একটি সমালোচনামূলক বিন্দু একাত্মতার এই ব্যবধান বা এ ঐ শেষ এর ব্যবধান
ক্রমাগত একটি ব্যবধান আছে এবং তাতে একটি সসীম সংখ্যা সমালোচনামূলক পয়েন্ট, তারপর, এটা attains তার সর্বোচ্চ এবং সর্বনিম্ন মান উপর এই ব্যবধান হয় একটি সমালোচনামূলক বিন্দু একাত্মতার এই ব্যবধান বা এ ঐ শেষ এর ব্যবধান
খোঁজা সর্বোচ্চ এবং সর্বনিম্ন মান ক্রমাগত ফাংশন ব্যবধান
উদাহরণ. 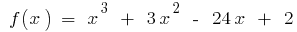 যখন
যখন 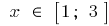
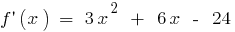
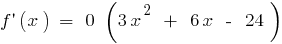 যদি
যদি 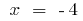 এবং যখন
এবং যখন 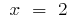
একটি প্রদত্ত রেখাংশ 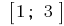 জন্যে শুধুমাত্র সমালোচনামূলক বিন্দু
জন্যে শুধুমাত্র সমালোচনামূলক বিন্দু 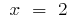
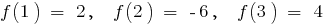

- খুঁজে বের করতে ডেরিভেটিভ

- এটি সমালোচনামূলক পয়েন্ট (
 বা না বিদ্যমান)
বা না বিদ্যমান) - নির্বাচন গুরুত্বপূর্ণ পয়েন্ট যে অন্তর্গত একটি প্রদত্ত রেখাংশ
- নিরূপণ, ফাংশন মান এ সমালোচনামূলক পয়েন্ট এবং শেষ এর ব্যবধান
- দুটি তুলনা মান এবং পছন্দ করে নিন ক্ষুদ্রতম ও বৃহত্তম

 আছে যে একটি extremum
আছে যে একটি extremum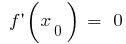 বা না আছে
বা না আছে