ধারণা দ্বিতীয় ডেরিভেটিভ



ধরুন ফাংশন  আছে একটি অমৌলিক
আছে একটি অমৌলিক  , এ সব পয়েন্ট থেকে কিছু ব্যবধান. এই ব্যুৎপন্ন, ঘুরে, একটি ফাংশন হয়
, এ সব পয়েন্ট থেকে কিছু ব্যবধান. এই ব্যুৎপন্ন, ঘুরে, একটি ফাংশন হয় 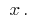 , তাহলে ফাংশন
, তাহলে ফাংশন  পৃথকীকৃত হয়, তার ডেরিভেটিভ বলা হয়, দ্বিতীয় ডেরিভেটিভ
পৃথকীকৃত হয়, তার ডেরিভেটিভ বলা হয়, দ্বিতীয় ডেরিভেটিভ  এবং সূচিত
এবং সূচিত 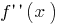 (বা
(বা 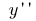 )
)
উদাহরণ. 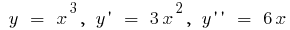
ধারণা convexity, খোল এবং আনতি পয়েন্ট অফ দ্য গ্রাফ funct
যাক ফাংশন  সংজ্ঞায়িত করে ব্যবধান
সংজ্ঞায়িত করে ব্যবধান 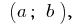 এবং পয়েন্ট
এবং পয়েন্ট 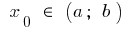 একটি নির্দিষ্ট ব্যুৎপন্ন. তারপর সময়সূচী এই ফাংশন সময়ে
একটি নির্দিষ্ট ব্যুৎপন্ন. তারপর সময়সূচী এই ফাংশন সময়ে 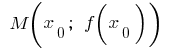 ধরে রাখতে পারেন, স্পর্শক
ধরে রাখতে পারেন, স্পর্শক
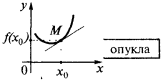
যদি কিছু আশপাশ বিন্দু  সব পয়েন্ট বক্ররেখা গ্রাফ এর একটি ফাংশন
সব পয়েন্ট বক্ররেখা গ্রাফ এর একটি ফাংশন  (ব্যতীত জন্য পয়েন্ট
(ব্যতীত জন্য পয়েন্ট  ) থাকা উপরে, স্পর্শক লাইন, তারপর, আমরা বলতে যে বক্ররেখা (ফাংশন) এ নির্দেশ
) থাকা উপরে, স্পর্শক লাইন, তারপর, আমরা বলতে যে বক্ররেখা (ফাংশন) এ নির্দেশ  করা হয়, উত্তল (আরো স্পষ্ট করে, কঠোরভাবে উত্তল). এছাড়াও, এটা কখনও কখনও বলেন যে এই ক্ষেত্রে ফাংশন গ্রাফ
করা হয়, উত্তল (আরো স্পষ্ট করে, কঠোরভাবে উত্তল). এছাড়াও, এটা কখনও কখনও বলেন যে এই ক্ষেত্রে ফাংশন গ্রাফ  হয়, উত্তল নিচে
হয়, উত্তল নিচে
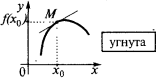
যদি কিছু আশপাশ বিন্দু  সব পয়েন্ট বক্ররেখা ছাড়া (পয়েন্ট
সব পয়েন্ট বক্ররেখা ছাড়া (পয়েন্ট  ) থাকা নিচে, স্পর্শক, তারপর, আমরা বলতে যে বক্ররেখা (ফাংশন) সময়ে
) থাকা নিচে, স্পর্শক, তারপর, আমরা বলতে যে বক্ররেখা (ফাংশন) সময়ে  হয় potou (বা, বরং কঠোরভাবে potou). এছাড়াও, এটা কখনও কখনও বলেন যে এই ক্ষেত্রে ফাংশন গ্রাফ হয়, উত্তল আপ
হয় potou (বা, বরং কঠোরভাবে potou). এছাড়াও, এটা কখনও কখনও বলেন যে এই ক্ষেত্রে ফাংশন গ্রাফ হয়, উত্তল আপ
যদি বিন্দু  x-অক্ষের উপর আছে যে সম্পত্তি যদি যুক্তির
x-অক্ষের উপর আছে যে সম্পত্তি যদি যুক্তির  মাধ্যমে বক্ররেখা
মাধ্যমে বক্ররেখা  পাস, এক পাশ থেকে অন্য স্পর্শক, তারপর বিন্দু
পাস, এক পাশ থেকে অন্য স্পর্শক, তারপর বিন্দু  বলা হয়, আনতি বিন্দু ফাংশন
বলা হয়, আনতি বিন্দু ফাংশন  পয়েন্ট বক্ররেখা
পয়েন্ট বক্ররেখা 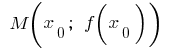 — আনতি বিন্দু গ্রাফ এর একটি ফাংশন
— আনতি বিন্দু গ্রাফ এর একটি ফাংশন 
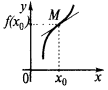
 বিন্দু আনতি গ্রাফ এর একটি ফাংশন
বিন্দু আনতি গ্রাফ এর একটি ফাংশন
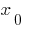 আনতি বিন্দু ফাংশন
আনতি বিন্দু ফাংশন
কিছু আশপাশ বিন্দু  : যখন
: যখন 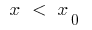 বক্ররেখা নীচে হয়, স্পর্শক, এবং যখন
বক্ররেখা নীচে হয়, স্পর্শক, এবং যখন 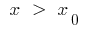 বক্ররেখা উপরে হয়, স্পর্শক (বা তদ্বিপরীত)
বক্ররেখা উপরে হয়, স্পর্শক (বা তদ্বিপরীত)
The study of the function of the bulge, unott এবং আনতি পয়েন্ট
উদাহরণ. 
সুযোগ: 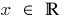
ফাংশন হয়, ক্রমাগত প্রতিটি বিন্দু তার ডোমেইন এর সংজ্ঞা
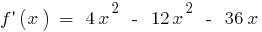
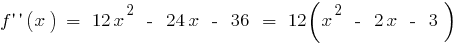
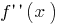 সেখানে সমগ্র সুযোগ
সেখানে সমগ্র সুযোগ
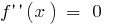 যখন
যখন 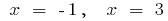
মধ্যে ব্যবধান 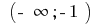 , এবং ব্যবধান
, এবং ব্যবধান 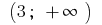 একটি ফাংশনের গ্রাফ
একটি ফাংশনের গ্রাফ  convexity নির্দেশ কৃত
convexity নির্দেশ কৃত 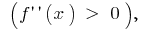 এবং ব্যবধান
এবং ব্যবধান  গ্রাফ ফাংশন
গ্রাফ ফাংশন  পাঠানো আচমকা
পাঠানো আচমকা 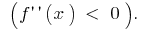
আনতি পয়েন্ট: 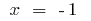 আমি
আমি 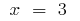 (এই পয়েন্ট
(এই পয়েন্ট 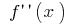 পরিবর্তন সাইন)
পরিবর্তন সাইন)
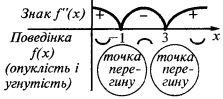
- খুঁজে পেতে সুযোগ এবং অন্তর যা ফাংশন ক্রমাগত
- এটি দ্বিতীয় ডেরিভেটিভ
- এটি একটি অভ্যন্তরীণ বিন্দু যেখানে নির্ণয়
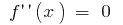 বা না আছে
বা না আছে - মার্ক ফলে পয়েন্ট, সুযোগ খুঁজে চিহ্ন দ্বিতীয় ডেরিভেটিভ এবং আচরণের উপর ফাংশন প্রতিটি ব্যবধান, যা splits সংজ্ঞা এলাকায়
- রেকর্ড করার জন্য পছন্দসই ফলাফল নিয়ে গবেষণা (অন্তর এর convexity এবং গোলাকার ফাঁপা বস্তুর ভিতর, এবং আনতি পয়েন্ট)

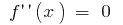 বা না আছে
বা না আছে