সংজ্ঞা:যদি একটি ফাংশন  সংজ্ঞায়িত একটি ব্যবধান
সংজ্ঞায়িত একটি ব্যবধান  এবং
এবং 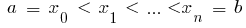 তারপর একটি নির্দিষ্ট সমাকলন একটি ফাংশন এর
তারপর একটি নির্দিষ্ট সমাকলন একটি ফাংশন এর  একটি ব্যবধান
একটি ব্যবধান  হয় একটি সংখ্যা সমান সীমা অবিচ্ছেদ্য সমষ্টি
হয় একটি সংখ্যা সমান সীমা অবিচ্ছেদ্য সমষ্টি 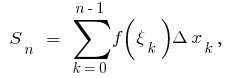 যেখানে
যেখানে 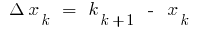 f
f 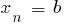
যে
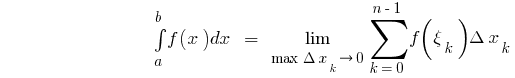
যেখানে 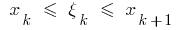 আমি
আমি 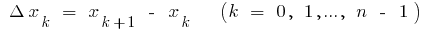
এর নির্মাণ অবিচ্ছেদ্য অঙ্কের জন্য উদাহরণ নির্ণয় এলাকার বক্ররেখা ট্র্যাপিজয়েড
যাক, সেগমেন্ট  সেট করা হয়, একটি অবিচ্ছেদ্য এবং অবিচ্ছিন্ন ফাংশন
সেট করা হয়, একটি অবিচ্ছেদ্য এবং অবিচ্ছিন্ন ফাংশন 
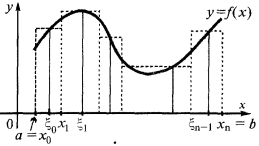
নির্ধারণ করার জন্য এলাকা, বক্ররেখা ট্র্যাপিজয়েড (bounded বক্ররেখা 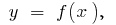 অক্ষ
অক্ষ 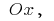 এবং সোজা,
এবং সোজা,  এবং
এবং 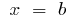 ), বিভক্ত কাটা
), বিভক্ত কাটা  পয়েন্ট
পয়েন্ট 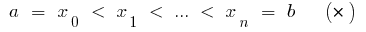
উপর 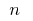 অংশ নির্বাচিত প্রতিটি প্রাপ্ত আংশিক অংশ
অংশ নির্বাচিত প্রতিটি প্রাপ্ত আংশিক অংশ 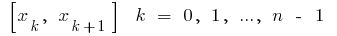 নিয়ে একটি অবাধ বিন্দু
নিয়ে একটি অবাধ বিন্দু 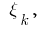 গণনা মান
গণনা মান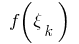 ফাংশন
ফাংশন  এ এই পয়েন্ট এবং ফর্ম সমষ্টি
এ এই পয়েন্ট এবং ফর্ম সমষ্টি 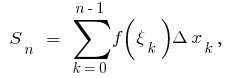 যেখানে
যেখানে 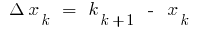
এই পরিমাণ সমান সমষ্টি এলাকার ছায়াময় আয়তক্ষেত্র বলা হয়, অবিচ্ছেদ্য সমষ্টি.
এখন যদি সংখ্যা বিভাজক পয়েন্ট বৃদ্ধি পায়, অনির্দিষ্টকালের জন্য, এবং দৈর্ঘ্য সর্বোচ্চ (সর্বোচ্চ) আংশিক কাটা পার্টিশন থাকে শূন্য, এবং মূল্য 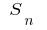 থাকে একটি নির্দিষ্ট সীমা
থাকে একটি নির্দিষ্ট সীমা  উপর নির্ভর করে না পদ্ধতি বিভাগ
উপর নির্ভর করে না পদ্ধতি বিভাগ 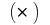 এবং পছন্দমত পয়েন্ট
এবং পছন্দমত পয়েন্ট 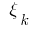 উপর আংশিক অংশ, তারপর মান
উপর আংশিক অংশ, তারপর মান 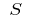 বলা হয়, এলাকার বক্ররেখা ট্র্যাপিজয়েড, অর্থাৎ
বলা হয়, এলাকার বক্ররেখা ট্র্যাপিজয়েড, অর্থাৎ 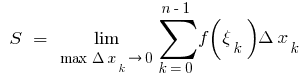
সূত্র - নিউটন Leibniz
যদি ফাংশন  সংজ্ঞায়িত এবং ক্রমাগত ব্যবধান
সংজ্ঞায়িত এবং ক্রমাগত ব্যবধান  এবং
এবং 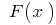 তার অবিচ্ছেদ্য (অর্থাৎ
তার অবিচ্ছেদ্য (অর্থাৎ 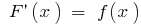 ), তারপর
), তারপর 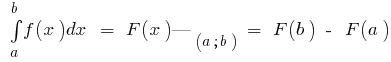
উদাহরণ. হিসাবে 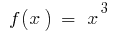 এক আদিম
এক আদিম 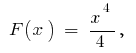 তারপর
তারপর 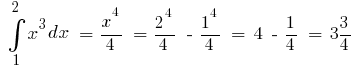
মৌলিক বৈশিষ্ট্য, নির্দিষ্ট সমাকলন
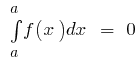
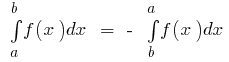
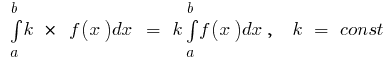
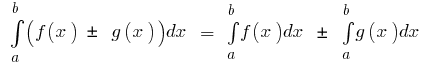
- যদি
 একত্রিত
একত্রিত  এবং
এবং 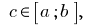 তারপর
তারপর
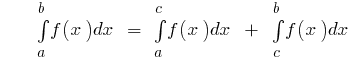

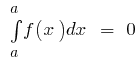
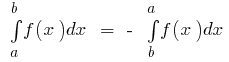
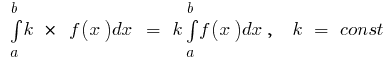
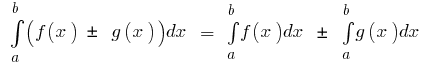
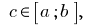 তারপর
তারপর