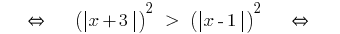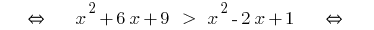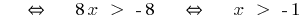সংজ্ঞা: একটি বৈষম্য সঙ্গে একটি একক পরিবর্তনশীল এবং  দুই এক্সপ্রেশন সঙ্গে এক পরিবর্তনশীল হয়, মার্কিন সঙ্গে সাইন
দুই এক্সপ্রেশন সঙ্গে এক পরিবর্তনশীল হয়, মার্কিন সঙ্গে সাইন 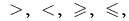 , যা তার সাধারণ ফর্ম ভালো লেখা হয়:
, যা তার সাধারণ ফর্ম ভালো লেখা হয়: 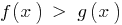
সংজ্ঞা: একটি রুট (বা rozvyazka অসাম্য)  বলা হয় এর মান একটি পরিবর্তনশীল দেখা যাচ্ছে যে একটি বৈষম্য মধ্যে সঠিক সংখ্যাসূচক সমতার.
বলা হয় এর মান একটি পরিবর্তনশীল দেখা যাচ্ছে যে একটি বৈষম্য মধ্যে সঠিক সংখ্যাসূচক সমতার.
Razvesti বৈষম্য মানে খোঁজার সব তার শিকড় (interchanges) বা দেখানোর জন্য যে, তারা না হয়.
এলাকার সম্ভবপর মান DHS বৈষম্য
সংজ্ঞা: এলাকায় অনুমোদিত মান (পরিসীমা সংজ্ঞা) বাধা বিপত্তি — মোট ব্যাপ্তি ফাংশন 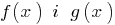 দাঁড়িয়ে, বাম এবং ডান অংশ সমীকরণ.
দাঁড়িয়ে, বাম এবং ডান অংশ সমীকরণ.
এটি এলাকার সম্ভবপর মান (odz)
উদাহরণ
সেট সমীকরণ: 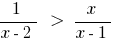
DHS: 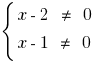 অর্থাৎ
অর্থাৎ 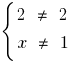
আপনি লিখতে পারেন এবং তাই 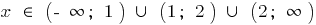 .
.
ত্বকের রুক্ষতা দুর হবে — প্রভাব
যখন rozwiazan বন্ধুরতা প্রভাব ব্যবহার করা হয় না (এবং ব্যবহার করা হয় সমতূল্য রূপান্তর), যেহেতু এটি সাধারণত অসম্ভব যাচাই করতে সব পেয়েছি rozvytku অসাম্য-পরিণতি.
সমতূল্য বৈষম্য
সংজ্ঞা: সমতূল্য (সমতুল্য) এবং বাধা বিপত্তি দুটি বাধা বিপত্তি, যার জন্য অনেক DHS আছে একই ফলাফল যে হয়, প্রতিটি সমাধান এর প্রথম বৈষম্য করা হয় rozvyazka দ্বিতীয়, এবং তদ্বিপরীত.
কিছু উপপাদ্য সম্পর্কে সমানভাবে প্রভাবশালী হয় সমীকরণ
উপপাদ্য 1: যদি এক অসাম্য সরাতে আরেকটি অংশ, পদ সঙ্গে বিপরীত সাইন, আমরা পেতে nervst সমতুল্য একটি দেওয়া (কোন সেট).
উপপাদ্য 2.1: যদি উভয় পক্ষের মধ্যে একটি বৈষম্য করা, গুন বা ভাগ দ্বারা একই ইতিবাচক পূর্ণসংখ্যা শূন্যের সমান না (বা এক এবং একই ফাংশন যে সংজ্ঞায়িত করা হয় এবং শূন্যের সমান না করে আইডি দেওয়া সমীকরণ), আমরা পেতে বৈষম্য সমপরিমাণ দেওয়া.
উপপাদ্য 2.2: যদি উভয় পক্ষের মধ্যে একটি বৈষম্য করা, গুন বা ভাগ দ্বারা একই VMA পূর্ণসংখ্যা শূন্যের সমান না (বা এক এবং একই ফাংশন সংজ্ঞায়িত করা হয়, যা, এবং WMA উপর odz দেওয়া সমীকরণ) এবং KRM পরিবর্তন করার জন্য, বৈষম্য সাইন করার জন্য, বিপরীত, আমরা পেতে বৈষম্য সমপরিমাণ দেওয়া.
উপপাদ্য 3.1: যদি উভয় পক্ষই 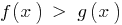 নিতে, বৃদ্ধি, ফাংশন
নিতে, বৃদ্ধি, ফাংশন 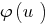 (সংরক্ষণের the sign of the বৈষম্য) এবং নেই কোন কমিয়ে আনায় এবং DHS - নির্দিষ্ট বৈষম্য, ফলে বৈষম্য
(সংরক্ষণের the sign of the বৈষম্য) এবং নেই কোন কমিয়ে আনায় এবং DHS - নির্দিষ্ট বৈষম্য, ফলে বৈষম্য 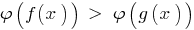 করা সমতুল্য উল্লেখিত ( DHS).
করা সমতুল্য উল্লেখিত ( DHS).
উপপাদ্য 3:2 হলে, উভয় পক্ষের 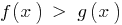 নিতে স্পটলাইট ফাংশন,
নিতে স্পটলাইট ফাংশন, 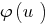 পরিবর্তন, চিহ্ন, অসাম্য এবং নেই কোন কমিয়ে আনায় এবং DHS - নির্দিষ্ট বৈষম্য, ফলে বৈষম্য
পরিবর্তন, চিহ্ন, অসাম্য এবং নেই কোন কমিয়ে আনায় এবং DHS - নির্দিষ্ট বৈষম্য, ফলে বৈষম্য 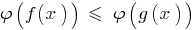 করা সমতুল্য উল্লেখিত ( DHS).
করা সমতুল্য উল্লেখিত ( DHS).
Corollaries এর উপপাদ্য সম্পর্কে সমানভাবে প্রভাবশালী হয় অসাম্য
ফল: কারণ ফাংশন হয় 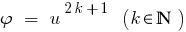 monotonically বৃদ্ধি,তারপর
monotonically বৃদ্ধি,তারপর
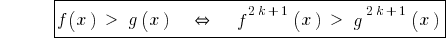 .
.
উপস্থাপনা উভয় অংশ অদ্ভুত প্রাকৃতিক ডিগ্রী, ফলে বৈষম্য সমপরিমাণ দেওয়া.
ফল: কারণ ফাংশন হয় 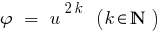 monotonically বৃদ্ধি শুধুমাত্র যদি
monotonically বৃদ্ধি শুধুমাত্র যদি 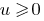 ক্ষেত্রে,যখন উভয় পক্ষের মধ্যে একটি বৈষম্য newmn, উদ্ধরণ দ্বারা উভয় অংশের প্রাকৃতিক থেকে এমনকি ডিগ্রী পেতে Nernst সমতুল্য এই.
ক্ষেত্রে,যখন উভয় পক্ষের মধ্যে একটি বৈষম্য newmn, উদ্ধরণ দ্বারা উভয় অংশের প্রাকৃতিক থেকে এমনকি ডিগ্রী পেতে Nernst সমতুল্য এই.
উদাহরণ 1
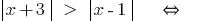 (উভয় অংশের newmn!)
(উভয় অংশের newmn!)