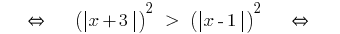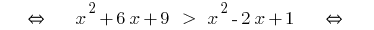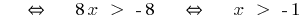Определение: Неравенство с одной переменной 
два выражения с переменной соединенные одним со знаком 
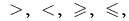которая в общем виде записывается так: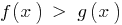 
Определение: Корнем (или розвязком) неравенства называется значение переменной, которое превращает неравенство в верное числовое равенство.
Розвязати неравенство — значит найти все его корни (развязки) или показать, что их нет.
Область допустимых значений ОДЗ неравенства
Определение: Область допустимых значений (область определения) неровности — общая область определения для функций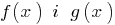 
, стоящих в левой и правой частях уравнения.
Найти область допустимых значений (ОДЗ)
Пример
Задано уравнение: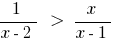 
ОДЗ: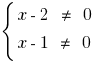 
, т. е.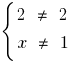 
, что можно записать и так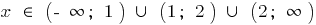 
.
Неровности — последствия
При розвязувнні неровностей последствия не используются (а используются равносильные преобразования), поскольку обычно невозможно выполнить проверку всех полученных розвязків неравенства-следствия.
Равносильные неравенства
Определение: Равносильны (эквивалентны) неровности — две неровности, которые на множестве ОДЗ имеют одни и те же развязки, то есть каждое решение первого неравенства является розвязком второй и, наоборот.
Некоторые теоремы о равносильности уравнений
Теорема 1: Если из одной части неравенства перенести в другую часть слагаемые с противоположным знаком, то получим нерівнсть, равносильное заданному (на любом множестве).
Теорема 2.1: Если обе части неравенства умножить или разделить на одно и то же положительное число, не равное нулю (или на одну и ту же функцию, которая определена и не равна нулю на ОДЗ заданного уравнения), то получаем неравенство равносильное заданному.
Теорема 2.2: Если обе части неравенства умножить или разделить на одно и то же відємне число, не равное нулю (или на одну и ту же функцию, которая определена и відємна на ОДЗ заданного уравнения) и, крм того, поменять знак неравенства на противоположный, то получим неравенство, равносильное заданному.
Теорема 3.1: Если от обеих частей неравенства 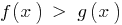взять возрастающую функцию 
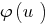(сохранив знак неравенства) и при этом не происходит сужение ОДЗ заданного неравенства, то полученное неравенство 
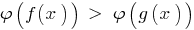будет равносильно заданному (на ОДЗ).
Теорема 3:2 Если от обеих частей неравенства 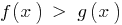взять нисходящую функцию 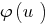, изменив знак неравенства, и при этом не происходит сужение ОДЗ заданного неравенства, то полученное неравенство 
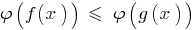будет равносильно заданному (на ОДЗ).
Следствия из теорем о равносильности неравенств
Следствие: Поскольку функция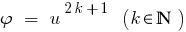 
монотонно возрастает,то
.
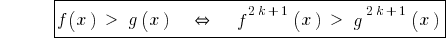При поднесении обеих частей до нечетного натурального степень получаем неравенство, равносильное данному.
Следствие: Поскольку функция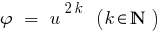 
монотонно возрастает лишь при 
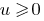,то в случае, когда обе части неравенства невідємні, при подъеме обеих его частей до четного натурального степень получаем нерінвість, равносильное данному.
Пример 1
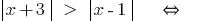(обе части невідємні!)
