Понятие системы и ее розвязків
Определение: Линейные уравнения с двумя переменными — это уравнение типа 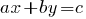 , где
, где  и
и  — переменные,
— переменные, 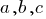 — заданные числа, для уравнения.
— заданные числа, для уравнения.
Решением уравнения с двумя переменными называется пара значений переменных, которая превращает уравнение в верное числовое равенство. Эта пара значений переменных называется решением уравнения.
Если два неизвестных значения связаны не одним, а двумя уравнениями, то эти уравнения — система линейных уравнений с двумя переменными.
Решением системы уравнений с двумя переменными называется пара чисел, при которых каждое уравнение системы превращается в верное числовое равенство.
Системы линейных уравнений с двумя переменными можно решить тремя способами:
- Графічнии способ решению систем линейных уравнений — в одной системе координат строятся графики двух уравнений, и координаты точки пересечения графиков соответствуют корням уравнений. Наиболее наглядный способ, но имеет и наибольшие погрешности при вычислениях, поскольку точность определения координат точки зависит от масштаба изображения. Особенно сложным является решение систем, когда коэффициенты или корни уравнения — дробные числа.
- Способ подстановки — наиболее универсальный из всех способов решения линейных уравнений с двумя переменными. Он используется практически для всех типов систем уравнений. Способ подстановки заключается в том, что из каждого уравнения одно из неизвестных выражается через другое неизвестное, и так до тех пор, пока не получим результирующее уравнение, в котором будет только одно неизвестное.
- Способ алгебраического сложения часто используется тогда, когда коэффициенты при одном из неизвестных численно равны или их можно свести к одинаковой числовой величины в рівносильному уравнении без сложных вычислений. Способ алгебраического сложения заключается в получении равносильного уравнения с одной из данных линейных уравнений. Добавляя два уравнения осуществляем переход к одному уравнению с одним неизвестным.
Решение систем линейных уравнений
Графический способ решения систем линейных уравнений
Пример: Розвяжіть уравнения: 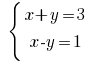
Решению:
Строим графики на плоскости: 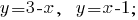
Построив графики систем линейных уравнений, увидим, что графики пересекаются в точке А 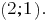
Ответ: 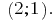
Способ подстановки для решения систем линейных уравнений
Пример: Розвяжіть уравнения: 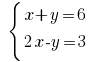
Розв'зування:
Из первого уравнения выражаем 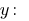
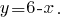
А полученное выражение подставляем во второе уравнение системы:
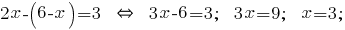
Полученное значение  подставляем в выражение
подставляем в выражение 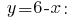
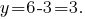
Ответ: 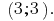
Способ сложения для решения систем линейных уравнений
Пример: Розвяжіть уравнения: 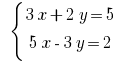
Решения:
Должны избавиться от переменной 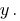 Умножаем почленно первое уравнение системы на
Умножаем почленно первое уравнение системы на 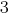 , а второе – на
, а второе – на 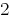 .
.
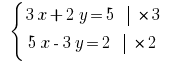
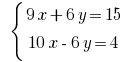
Почленно добавляем линейные уравнения и получаем: 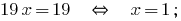
Находим значение  из первого уравнения системы:
из первого уравнения системы: 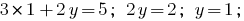
Ответ: 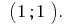
Замечание: В методе добавления можно умножать не только на положительные числа, а и на отрицательные.
Также Вы можете ознакомиться с информацией о системы линейных уравнений здесь
