線形方程式

のコンセプトシステムとそのrozvytku

定義: 線形方程式 と二つの変数が式のタイプ 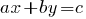の場 と して変数 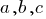の設定の表示件数を増やす表示件数を減らの方程式です。

の解決方程式の解の二つの変数 の変数が 式の に正しい数値を進めていきます。 このペアの値を変数と呼び解決の方程式です。

の場合は不明でないかどうかについて合理的な一方程式、そしてこれらの方程式— システムの線形方程式 と二つの変数です。

液システムの方程式 と二つの変数はペアの数によって 方程式のシステム に変換しtrue数値型を進めていきます。

システムの線形方程式の二つの変数を解決することができ、まず言語運用能力が不可欠です。

1. Grafone方法で解決システムの線形方程式 と同じ座標系のグラフの方程式の座標のポイントの交差点をグラフに対応のルーツ方程式です。 目の前にある、ことりと触れ合うには、最大誤差の計算の精度を決定座標のポイントの規模によって異なりのイメージです。 特に難しいでは のソリューションは、システムの場合、係数のルーツは、数式—数です。
2. 方法のルックアップ は最も汎用性のすべてのメソッドの解決線形方程式の二つの変数です。 では、ほとんどのシステムの方程式です。 の方法での代替 の 各方程式 からの未知の表現も不明で、それまでまでの方程式を一つだけます。
3. 方法での代数のほか、 多くの場合の係数の未知数値と同等以上のものを削減できる同じ数値runoilija式な複雑な計算をします。 方法での代数のほか、 取得の方程式の線形方程式です。 追加の両方程式系に進む一方程式の解の一不明である。

解決システムの線形方程式

グラフィカル方法を解決システムの線形方程式

例: Rozwarte式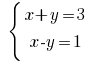

【解決

構築グラフを平面：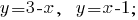

ビルグラフシステムの線形方程式をまとめると、グラフの交差点にあ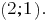

回答: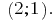

方法に置換すると解決システムの線形方程式

例: Rozwarte式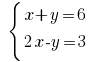

Rosvサバンナ:

の式で表現いたしました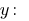

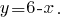
の表現に置換の方程式をシステム

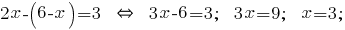
この値 は置換を表現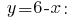

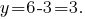
回答: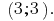

方法のほか、解決システムの線形方程式

例: Rozwarte式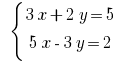

ソリューション

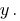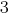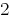く変 poslano掛けの方程式をシステム の第二に します。

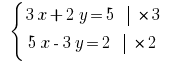
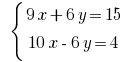
Pocino追加の線形方程式です: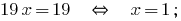

の値 の最初の方程式をシステム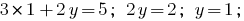

回答: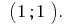

備考 方法を追加できかけのみならず正の数-負になります。

を見ることができま情報 システムの線形方程式は こちら