の語の継続性機能
の十分条件のための高機能化
た場合の各点の間隔 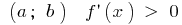 は、この機能 は増加して この間隔
は、この機能 は増加して この間隔
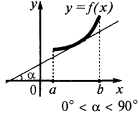
の十分条件を減らすための機能
た場合の各点の間隔 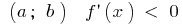 の 減少 この間隔
の 減少 この間隔
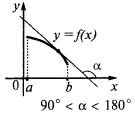
な趣旨の発言があった。 これらの条件は十分な必要条件の成長-減衰機能
めの必要十分条件の恒常性の機能
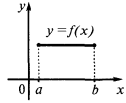
機能  は一定間隔
は一定間隔 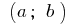 の場合だけが
の場合だけが  すべてのポイントの間隔
すべてのポイントの間隔
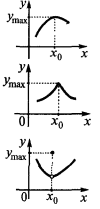
の極端な(最大、最低限の機能
の最大のポイント
個人情報の定義について の点  を定義する機能の
を定義する機能の  呼び a最大のポイントは この機能の場合
呼び a最大のポイントは この機能の場合 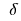 は近隣
は近隣 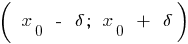 の点
の点  がすべて
がすべて 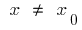 このことから近隣の不平等
このことから近隣の不平等 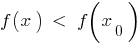
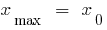 —の最大のポイント
—の最大のポイント
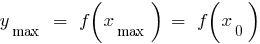 —max
—max
を最小限に
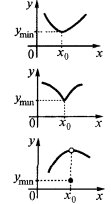
個人情報の定義について の点  を定義する機能
を定義する機能  は 最小点 のこの機能の場合
は 最小点 のこの機能の場合 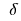 は近隣
は近隣 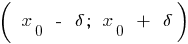 の点
の点  がすべて
がすべて 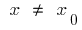 このことから近隣の不平等
このことから近隣の不平等 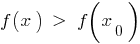
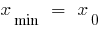 —最低点
—最低点
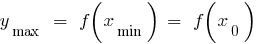 —最小
—最小
の臨界点
定義: 内装のポイントのドメインの定義機能の誘導体のゼロまたは存在しないという 重要な
必要な条件extremum
 —extremum点
—extremum点 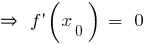 は
は 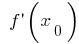 存在しない
存在しない
なもので、各ポイント  が
が 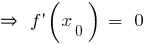 は
は 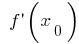 ずがありますextremum!)
ずがありますextremum!)
十分条件のextremum
の  サイン
サイン 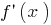 変動
変動 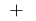 で
で 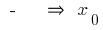 最大のポイント
最大のポイント
時点での  サイン
サイン 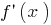 変更
変更  の
の 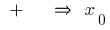 点の最小
点の最小
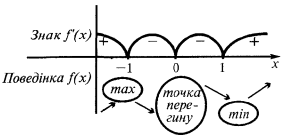
グラフの一例を示の機能  がextremum
がextremum
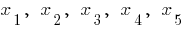 —臨界点
—臨界点
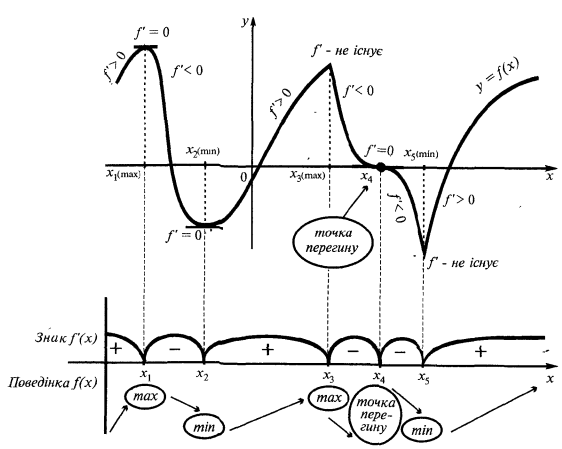
この研究の関数の単調性、極端
例です。 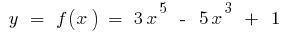
対象範囲: 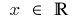
その機能は連続で、そのドメインの定義
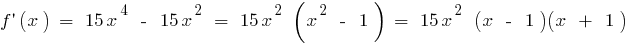
 あの全範囲
あの全範囲
 時
時 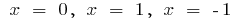
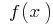 の増加と
の増加と 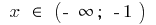 と
と 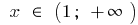
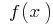 補助金の場合
補助金の場合 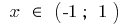
極端なポイント: 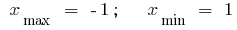
極端: 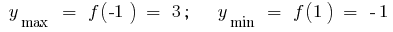
- のドメインの定義との間の機能連続
- の誘導体

- の重要なポイント、すなわち、内部ポイントする場所の決定
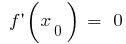 がない
がない - 表示は重要なポイントのドメインの定義は、サインの誘導体の自然の機能で各区間を分割を定義域
- 各ポイントであるかどうかを判定するのに高低はありませんextremum点
- 記録porni研究成果は、(間隔での単調性や極端)
最大値-最小値の継続的な機能の間隔
物件: この機能は  連続的にモニタリングする間隔とその有限数が重要なポイントは、それぞれの最大-最小値この間のいずれかで重要な点に所属すること間隔の端点の間隔
連続的にモニタリングする間隔とその有限数が重要なポイントは、それぞれの最大-最小値この間のいずれかで重要な点に所属すること間隔の端点の間隔
発見の最大値と最小値の継続的な機能の間隔
例です。 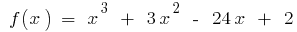 時
時 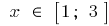
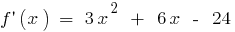
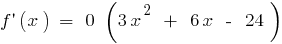 る場合
る場合 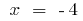 が
が 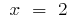
定のセグメント 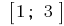 に帰属しみポイント
に帰属しみポイント 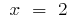
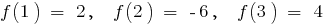

- の誘導体

- の重要なポイント(
 または存在しない)
または存在しない) - 選べる重要なポイントに所属している与えられたセグメント
- 計算の機能価値に重要なポイントの端点の間隔
- 比較して価値の最小と最大の

 がextremum
がextremum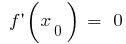 がない
がない