单调性和连续性的职能
一个充分条件增加功能
如果在每一地点的间隔 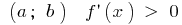 ,功能 是增加 在此时间间隔
,功能 是增加 在此时间间隔
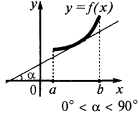
一个充分条件,减少的职能
如果在每一地点的间隔 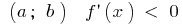 ,将能 减少 在此时间间隔
,将能 减少 在此时间间隔
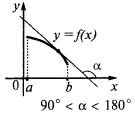
话。 这些条件仅仅是足够的,但不是必要条件对增长和减少功能
一个必要和充分条件的恒定的功能
一个功能  是恒定在一个时间间隔
是恒定在一个时间间隔 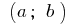 ,如果并且只有当
,如果并且只有当  所有点的时间间隔
所有点的时间间隔
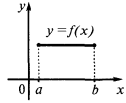
极值(最大值和最低值)的功能
大点
定义: 点  的定义功能
的定义功能  是所谓的 一个大点 的这一功能,如果有
是所谓的 一个大点 的这一功能,如果有 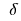 一个邻居
一个邻居 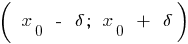 点
点  ,对于所有
,对于所有 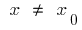 从这一地区的不平等
从这一地区的不平等 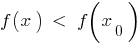
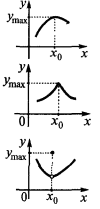
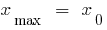 —大点
—大点
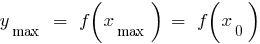 —max
—max
点的最低
定义: 点  的定义功能
的定义功能  被称为 最低点 的这一功能,如果有
被称为 最低点 的这一功能,如果有 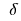 一个邻居
一个邻居 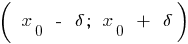 点
点  ,对于所有
,对于所有 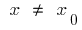 从这一地区的不平等
从这一地区的不平等 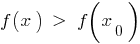
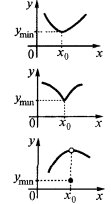
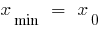 —最低点
—最低点
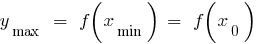 —最低
—最低
临界点
定义: 内政部分领域的定义功能的衍生物是零或不存在称为 关键的
必要条件的一个极点
 —的极值点
—的极值点 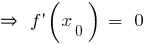 或
或 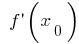 不存在
不存在
(但不在每个点  在那里
在那里 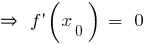 或者
或者 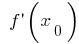 不会有一个极点!)
不会有一个极点!)
充分条件的极值
在  签署
签署 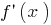 变更
变更 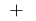 在
在 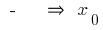 点最大
点最大
在  签署
签署 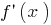 变更
变更 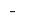 在
在 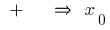 点的最低
点的最低
例的函数的曲线图  ,这具有极值
,这具有极值
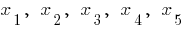 —关键点
—关键点
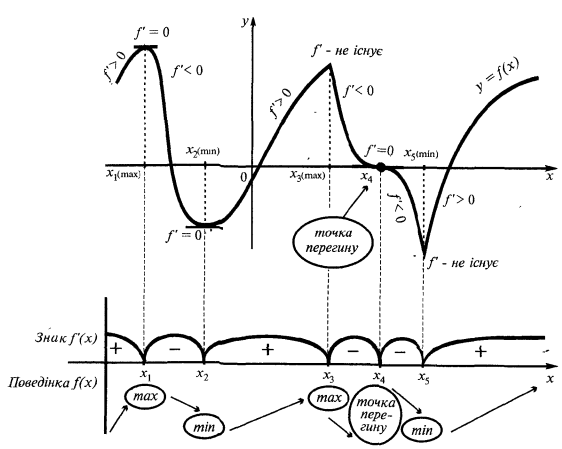
研究功能上的单调性和极
例。 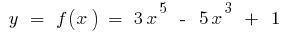
范围: 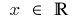
该职能是连续的每一点域的定义
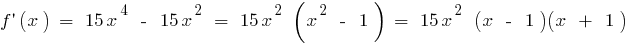
 存在的整个范围
存在的整个范围
 时
时 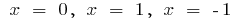
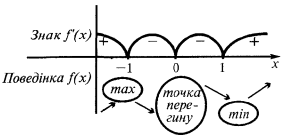
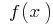 随
随 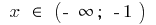 和
和 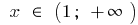
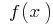 消退的时候
消退的时候 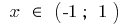
极端分: 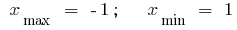
极端: 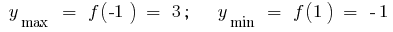
- 找域的定义和间隔的功能是连续的
- 找到的衍生物

- 找到关键点,即内部分确定
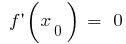 或不存在的
或不存在的 - 表示关键点上域的定义,找到标志的衍生物和自然功能,在每个时间间隔,分区域的定义
- 对于每个关键点确定它是否是高或低,或者是不是一种极值点
- 记录porni的结果的研究(间隔时间的单调性和极值)
最大值和最小值的连续职能的时间间隔
财产: 如果该职能是  连续时间间隔,并有其中的有限数量的临界点,然后就达到其最大值和最小值,在此时间间隔无论是在一个关键点属于这个时间间隔或在终点的时间间隔
连续时间间隔,并有其中的有限数量的临界点,然后就达到其最大值和最小值,在此时间间隔无论是在一个关键点属于这个时间间隔或在终点的时间间隔
发现的最大值和最小值的连续职能的时间间隔
例。 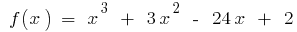 时
时 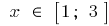
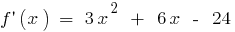
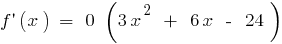 如果
如果 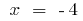 和当
和当 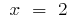
一定段 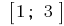 只属于临界点
只属于临界点 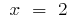
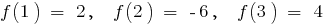

- 找到的衍生物

- 找到关键点(
 或不存在)
或不存在) - 选择临界点,属于某个给定的段
- 计算函数值的关键点和终点的时间间隔
- 比较这两个价值观和选择最小和最大的

 ,这具有极值
,这具有极值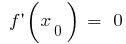 或不存在的
或不存在的