系统的线性方程

这一概念的系统及其rozvytku

定义： 线性公式 有两个变量是一个方程式 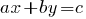在哪里 和 是变量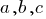， —这组数字为的公式。

的解决方案方程式用两个变量 是一个对变量，而成 本的公式 纳入正确的数值的平等。 这对价值的变量是称为解决该等式。

如果两名身份不明的价值观都不是一个而是两个方程，然后这些方程— 系统的线性公式 有两个变量。

解决方案的系统的公式 有两个变量是一对数字，其中每一个 公式的系统 转换成真正的数字的平等。

系统的线性公式有两个变量可以解决在三个方面：

1. Grafone方法解决系统的线性等式 ，在同样的协调系统图的两个方程和坐标点的交叉关系图应根源的方程式。 最明显的方式，但是具有最大的错误计算，因为准确确定的坐标点取决于比例尺的图像。 特别困难的是 解决系统，在该系数或者根本方程数字。
2. 方法查找 最灵活的所有方法的解决线性公式有两个变量。 它是用于几乎所有类型的系统的方程式。 该方法取代 的是这的 每个方程 从一个未知的是通过表示的另一个未知的，并且因此直到那时，直到获得结果方程式中的其中只有一个未知数。
3. 方法的代数外 时，通常使用的系数一个未知数值上相等或者它们可以减少相同的数值在runoilija式而无需复杂的计算。 方法的代数外 获得相当于方程式之一，这些线性方程式。 添加两个方程式进行到的一个等式的一个未知数。

解决系统的线性方程

图形的方法解决系统的线性方程

例如： Rozwarte方程式：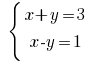

方案：

建立图表中的飞机：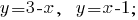

建筑物的图表系统的线性等式，我们看到图相交的点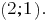

回答：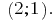

该方法的替代解决系统的线性方程

例如： Rozwarte方程式：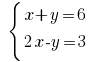

Rosv热带稀树草原为：

从第一个方程式我们表示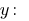

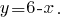
和所得的表达是取代为第二个公式的系统：

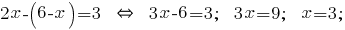
得到的数值 代入表达式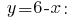

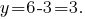
回答：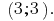

方法加以解决系统的线性方程

例如： Rozwarte方程式：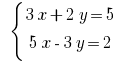

方案：

需要摆脱的一个变量 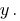poslano乘的第一个公式的系统 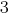，第二个–对 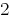的。

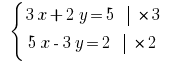
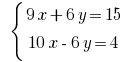
Pocino增加的线性公式获得：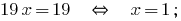

找到价值 的第一个公式的系统：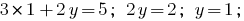

回答：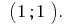

注： 方法增加，可以成倍增加，不仅在正数和负数。

你还可以找到有关的信息 系统的线性方程式 在这里