这一概念的不理性的方程式
定义: 一个不合理的等式  是一个公式包含的变量在根签署
是一个公式包含的变量在根签署  的第一个学位。
的第一个学位。
解决的不理性的方程式
在介绍这两个部分的方程式的程度是奇(1,3,5,7....) 得到的等式是相当于给定( DHS)
实例1:
Rozwarte方程式: 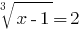
方案: 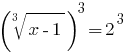
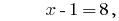
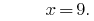
回答:
在介绍的两侧双学位(2,4,6,8....) 可能会出现多余的根源,这将消除检查。
实例2:
Rozwarte方程式: 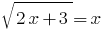
方案: 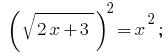
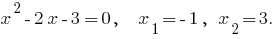
检查: 当你 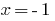 已经
已经 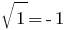 不是一个正确的公式,因此,
不是一个正确的公式,因此, 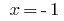 是一个无关的根源。
是一个无关的根源。
如果你 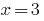 们
们 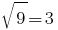 -一个真正的平等,因此,
-一个真正的平等,因此, 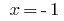 是根的给予等式。
是根的给予等式。
回答: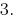
如果方程式中的可变发生在相同的形式,suchno相应的表达变为标志的一个封信(一个新的变量)。
实例3:
Rozwarte方程式: 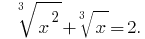
解决方案:让我们表示 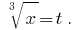 然后
然后 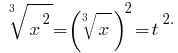
我们获得的方程式: 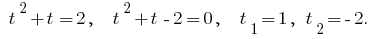
反对取代: 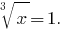 那么
那么  ,或者
,或者 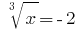 这里
这里 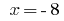 的。
的。
如果你 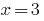 们
们 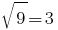 -一个真正的平等,因此,
-一个真正的平等,因此, 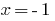 是根的给予等式。
是根的给予等式。
回答: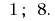
- 随着两个部分的方程式是不合理到一定程度上
- 使用变化的变量
