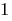对数方程

定义： 数公式 —一个方程式在哪些变量是根据签署 的对数..

那么好能够rozwiazywanie对数公式，需要能够控制 的基准比对数。

相当于改造的简单对数方程式。

 

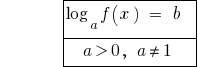
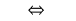
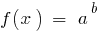
由于 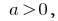在 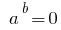马里人口及健康调查和因此最初的公式自动得到考虑。

 

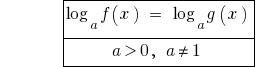
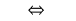
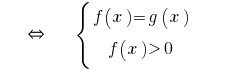或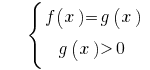

实例的解决方案的最简单的方程的对数

 

例1

Rozwarte方程式：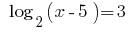

方案：

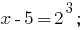
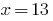
回答：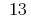

 

例2

Rozwarte方程式：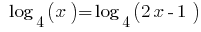

方案：

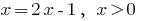(人口与健康调查也被认为是)

然后 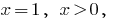就是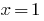

回答：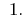

该方案是更复杂的方程的对数

1. 使用的公式和作用
2. 使用的属性有关的功能
3. 使用 相当于转换

作为razvesti对数公式

使用 公式的对数值和增效 降低的等式的一个简单的(考虑最初的人口与健康调查并确保不会失去根源的时候sujuan 马里人口及健康调查)了。 之后转变，如果它是不是可以减少到一个简单的对数的方程式我们正努力引入一个 变化的变量。

实例的解决方案方程的对数

 

例3(使用的公式，对数)

 

Rozwarte方程式：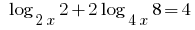

方案：

会基2,我们得到的等同的公式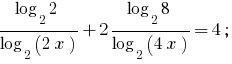

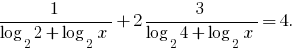
替换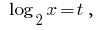

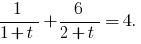
然后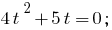

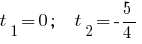
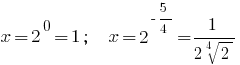
回答：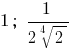

例4(使用特性的功能，对数)

 

Rozwarte方程式：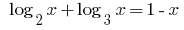

方案：

功能 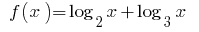增加，范围内 的总和两个增加的职能，以及 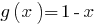来。 因此，所给的公式具有一个根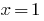

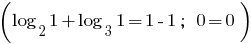
回答：