定义: 整数  分割的一个整数
分割的一个整数  ,如果有这样一个数字
,如果有这样一个数字 
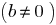 即
即 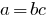 可。
可。
数  是所谓的 除数的 数量
是所谓的 除数的 数量  和数量
和数量  是 多 数
是 多 数  的。
的。
性能可分割的
- 如果
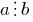 和
和 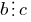 ,那么
,那么 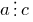 .
. - 如果
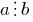 及
及 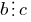 时,
时,  并
并  为任何整数,然后
为任何整数,然后 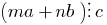 .
. - 如果
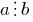 和
和 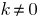 意
意 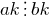 的。
的。 - 如果
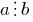 和
和 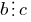 中,然后
中,然后  和
和 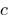 — vsampler 数。
— vsampler 数。
可分性的规则
可分割的2号
最后一位数字的号码是可分割的,由2(甚至).
整数  就是可分割的,由2名为 甚至是,它可以表示在形成
就是可分割的,由2名为 甚至是,它可以表示在形成 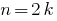 在那里
在那里 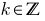 的。
的。
整数  就是不可分割的,由2是所谓的 奇怪而可以表示在形成
就是不可分割的,由2是所谓的 奇怪而可以表示在形成 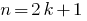 在那里
在那里 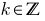 的。
的。
可分性的数量由3
总和的数字是可分割的,由3.
例如,数822. 它并不包含任何的三倍,但其数字 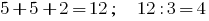 是可分割的,由3均匀,因此可分割的规则822可分割的,由3
是可分割的,由3均匀,因此可分割的规则822可分割的,由3 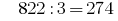 .
.
可分性的规则10
数结束 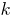 零。
零。
可分性的数字4
数量表示,通过的最后两位数字一定数目的是分割的,由4.
例如,数量 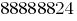 足够大部分学生在7年级。
足够大部分学生在7年级。
然而potrebno只需要检查可分割的4最后两位数字 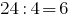 ,我们可以得出结论,88888824有一个除数的四。
,我们可以得出结论,88888824有一个除数的四。
可分性的数7
规则的可分割的7大的数字。 精神打破数成块的三位数字,开始从最后一位数字。 根据该规则,如果差值的总和块,站在甚至地方和总块,站在奇怪的地方,除以7的数字是可分割的,由7.
例如, 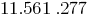
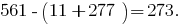
检查273中的规则
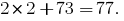
这个数字是"漂亮的"分为7. 所以检查可分割的一数由7和解决的例子可为多个规则。 他们每个人都有一些数字的某些优势,因此选择哪种方式更为直观和速度更快。
可分性的数5
最后一位数字的数字是0或5。
可分性的数量8
数量表示,通过的最后三位数字给出的数字是可由8.
可分性的人数9
数字的总和的数量可分割的,由9.
可分性的数字11
之间的差异总和的数字常在奇怪的地方(计数右到左的),并且总和的数字站在甚至个职位(从右到左计数)可分割的,由11.

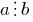 和
和 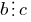 ,那么
,那么 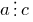 .
. 并
并 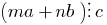 .
.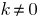 意
意 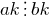 的。
的。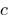 — vsampler 数。
— vsampler 数。