定义: 让是一个功能  上定义的整个数线。 数
上定义的整个数线。 数 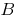 是所谓的限制的功能
是所谓的限制的功能  在
在 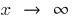 如果出于任何
如果出于任何 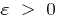 存在一个号码
存在一个号码 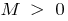 ,对所有
,对所有  满足条件
满足条件 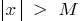 ,下面的不平等感到满意
,下面的不平等感到满意 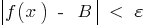
如果 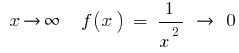 ,那就是,对大(绝对值)数值的
,那就是,对大(绝对值)数值的  数量
数量 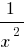 非常少不同的数0
非常少不同的数0

如果行为  是不同的
是不同的 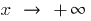 和
和 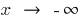 单独考虑
单独考虑 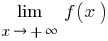 (定义中采取
(定义中采取 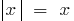 )和
)和 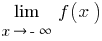 (定义采取
(定义采取 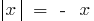 )
)


该限制的一个序列
由于 一序列 是一个功能的自然论点 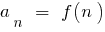 ,该定义的限制的顺序与
,该定义的限制的顺序与 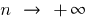 是完全相同的定义限制的功能在
是完全相同的定义限制的功能在 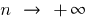
定义: 数 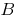 是所谓的限制序列
是所谓的限制序列 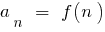 ,如果对于任何
,如果对于任何 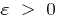 有这样的数量
有这样的数量 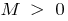 ,对所有
,对所有 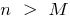 ,下面的不平等是满足
,下面的不平等是满足 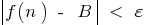 即
即

如果 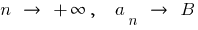 中,
中,

比较的指数增长指数和对数函数
- 时

 ,
,
就是

如果  ,当
,当 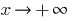 一个函数
一个函数 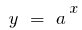 的增长速度超过了任何的指数函数
的增长速度超过了任何的指数函数 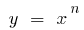 在那里
在那里  是天然的数量
是天然的数量
图形的方式,这种说法意味着 足够大的价值  的函数的曲线图
的函数的曲线图 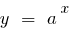 (
( 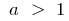 )以上的函数的曲线图
)以上的函数的曲线图 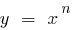
- 时
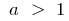
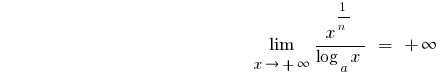 ,
,
就是
 ,
,
在大  ;
;
 ,
,
所以

如果  ,函数
,函数 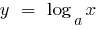 的增加速度慢于功能的
的增加速度慢于功能的 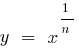 (和特别是慢于功能
(和特别是慢于功能 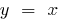 或功能
或功能 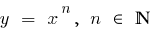 )
)
图形的方式,这种说法意味着 足够大的价值  的函数的曲线图
的函数的曲线图 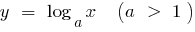 谎言之下的函数的曲线图
谎言之下的函数的曲线图 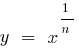 (特别是下面的图表功能
(特别是下面的图表功能 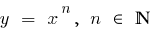 )
)
