定义: 多项式的一个变量  是一个多项式的形式,
是一个多项式的形式, 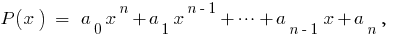 其中的
其中的 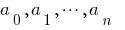 数值系数。
数值系数。
定义: 如果 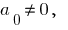 这一多项式是所谓 的多项式
这一多项式是所谓 的多项式  的第一个学位的相对变量
的第一个学位的相对变量  的。
的。
成员 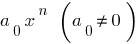 称为 一名高级成员 的多项式的
称为 一名高级成员 的多项式的 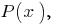 一个
一个 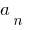 —它 免费件的。
—它 免费件的。
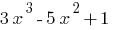 —多项式的第三位。
—多项式的第三位。
同等式中的一个变量
定义: 多项式的两个被称为 平等如果他们采取平等值的所有价值观的变量。
性能相同的平等的多项式在一个变量
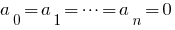
- 如果多项式
 是同等于零度(即有零价值观在所有价值观
是同等于零度(即有零价值观在所有价值观  ),那么其所有系数都等于零。
),那么其所有系数都等于零。 - 如果多项式的两个
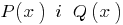 同等于(即,获得同样价值的所有价值观
同等于(即,获得同样价值的所有价值观  ),然后他们一致(即,他们的学位都是平等的系数相等的权力相等)。
),然后他们一致(即,他们的学位都是平等的系数相等的权力相等)。
分的多项式通过多项式
定义: 如果多项式的两个 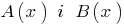 有可能找到多项式
有可能找到多项式 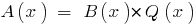 那
那 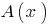 是分成
是分成  的。
的。
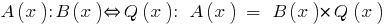
例
因为 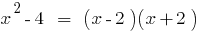 ,多项式
,多项式 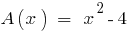 分通过的多项式
分通过的多项式 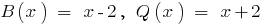
该司的多项式通过的多项式s斯泰西
定义: 多项式 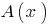 分通过的多项式
分通过的多项式  s斯泰西,如果你能找到一个对多项式
s斯泰西,如果你能找到一个对多项式 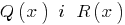 ,
, 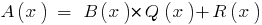 和程度的剩余部分
和程度的剩余部分 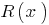 较小的程度
较小的程度  上。
上。
如果剩余部分 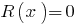 ,然后多项式
,然后多项式 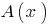 分通过的多项式的
分通过的多项式的  没有剩余)
没有剩余)
例
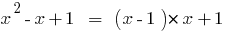
,
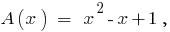
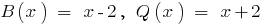
该司的多项式通过的多项式"区域"
该规则的分的多项式在一个变量
- 向地方成员的多项式与降指数的变量。
- 分享一名高级成员的股息的高级成员的分隔。
- 结果乘以除数与减去这一产品从红利。
- 获得的差异执行相同的操作:除名高级成员的高级成员分和结果再乘以因数,等等。 这一过程的继续,直到我得到的余额为零(如果一项多项式分由另一)或只要平衡没有得到多项式的程度小于学位的公约数。
理连续的
剩余部分的多项式  上doclen
上doclen 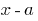 平等
平等 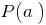
推论: 如果 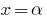 是一个根本的多项式
是一个根本的多项式  (即,
(即, 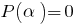 ),那么这多项式分割
),那么这多项式分割 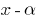 的。
的。
例
剩余部分的多项式 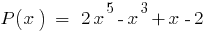 上doclen
上doclen 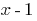 相等
相等 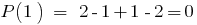 ,即
,即  分为
分为 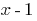 没有一个剩余部分。
没有一个剩余部分。
分割  成
成 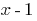 的"区域"霍纳的方案,我们会得到:
的"区域"霍纳的方案,我们会得到: 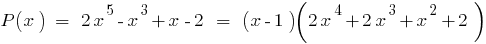

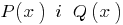 同等于(即,获得同样价值的所有价值观
同等于(即,获得同样价值的所有价值观