Definição: Многочленом de uma variável  é o tipo de polinômio
é o tipo de polinômio 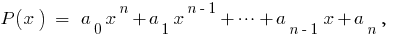 onde
onde 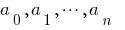 — coeficientes numéricos.
— coeficientes numéricos.
Definição: Se 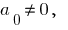 este polinômio é chamado de многочленом
este polinômio é chamado de многочленом  -oh grau relativamente a uma variável
-oh grau relativamente a uma variável  .
.
Membro 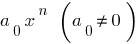 chamado de o mais velho membro do polinômio
chamado de o mais velho membro do polinômio 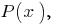 a
a 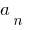 — lo um membro livre.
— lo um membro livre.
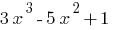 — um polinômio de terceiro grau.
— um polinômio de terceiro grau.
São identicamente iguais многочлены de uma variável
Definição: Dois polinômio são chamados são identicamente iguais, se eles aceitam a igualdade de valor quando todos os valores da variável.
A propriedade é idêntico a igualdade de fatorar polinômios de uma variável
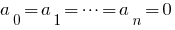
- Se um polinômio
 são identicamente igual a zero (ou seja, adquire um valor de zero quando todos os valores
são identicamente igual a zero (ou seja, adquire um valor de zero quando todos os valores  ), todos os coeficientes são iguais a zero.
), todos os coeficientes são iguais a zero. - Se dois polinômio
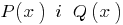 é a mesma coisa são iguais (ou seja, ganham o mesmo valor quando todos os valores
é a mesma coisa são iguais (ou seja, ganham o mesmo valor quando todos os valores  ), então eles são iguais (ou seja, seu grau de iguais e coeficientes iguais graus de igual).
), então eles são iguais (ou seja, seu grau de iguais e coeficientes iguais graus de igual).
A divisão de polinômio por polinômio
Definição: Se para os dois fatorar polinômios 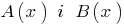 , você pode encontrar um polinômio
, você pode encontrar um polinômio 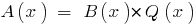 , dizem que
, dizem que 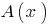 é dividido em
é dividido em  .
.
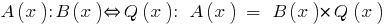
Exemplo
Porque 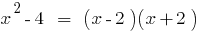 , então o polinômio
, então o polinômio 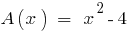 é dividido em um polinômio de
é dividido em um polinômio de 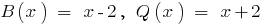
A divisão de polinômio por polinômio c остачею
Definição: um Polinômio 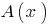 é dividido em um polinômio
é dividido em um polinômio  c остачею, se pode encontrar um par de fatorar polinômios
c остачею, se pode encontrar um par de fatorar polinômios 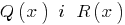 , que
, que 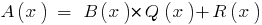 , com o grau de resíduo
, com o grau de resíduo 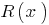 menor grau
menor grau  .
.
Se o resto 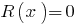 , o polinômio
, o polinômio 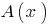 é dividido em um polinômio
é dividido em um polinômio  sem resíduo)
sem resíduo)
Exemplo
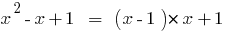
,
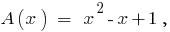
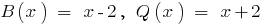
A divisão de polinômio por polinômio de "estar"
A regra de divisão fatorar polinômios de uma variável
- Colocar os membros fatorar polinômios com os que descem graus de variável.
- Dividir o membro sênior do делимого no membro sênior do divisor.
- O resultado multiplicado pelo divisor e é uma obra de subtrair делимого.
- Recebido diferença realizam uma operação semelhante: dividir o seu velho membro a membro sênior do divisor e o resultado é novamente multiplicado o divisor e assim por diante. Este processo continuam a dar, até se chegar a um saldo de zero (se um polinômio é dividido em outro) ou até que o restante não receberão um polinômio, o grau menor que o grau do divisor.
O Teorema De Carcaça Contínua
O resto da divisão de um polinômio  em двочлен
em двочлен 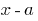 igual
igual 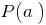
Conseqüência: Se 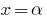 a raiz de polinômio
a raiz de polinômio  (isto é
(isto é 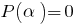 ), então o polinômio é divisível sem restante
), então o polinômio é divisível sem restante 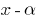 .
.
Exemplo
O resto da divisão de um polinômio 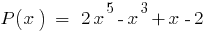 em двочлен
em двочлен 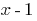 igual
igual 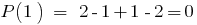 , ou seja,
, ou seja,  é dividido em
é dividido em 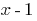 sem deixar resíduos.
sem deixar resíduos.
Поделив  em
em 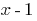 "estar" ou por um esquema de Горнера, temos:
"estar" ou por um esquema de Горнера, temos: 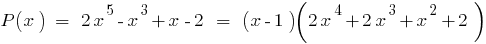

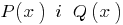 é a mesma coisa são iguais (ou seja, ganham o mesmo valor quando todos os valores
é a mesma coisa são iguais (ou seja, ganham o mesmo valor quando todos os valores