Frações decimais

Decimal — uma fração, o denominador comum de 10ⁿ, onde n é um número natural.

Gravado decimal é lido de acordo com o esquema

1	2	3	4	,	5	6	7	8
milhares de	centenas de	dezenas de	unidades		décimos	centésimos	milhares	десятитысячные

Por exemplo, decimal 10,436 de ler "dez inteiros e quatrocentos e trinta e seis milésimos".

Entre frações mais frequentemente usado na vida cotidiana, existem frações com знаменателями 10, 100, 1000 e т. д.

Por exemplo, 10 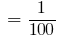kg,

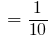1mm cm,

2cm 5mm 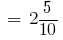ver e т. д.

O número de знаменателями 10, 100, 1000 e т. д. concordaram em gravar sem o denominador.
Primeiro a escrever a parte inteira de um, e então o numerador da fração. A parte inteira de um separam da parte decimal por uma vírgula.

Por exemplo, em vez de 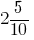escrever 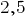(lêem-se: "2 inteiros e 5 décimos").

Um número qualquer, o denominador da fração do qual se expressa a unidade com um ou mais zeros, pode-se apresentar na forma de decimal de frações.

Se a fração certa, antes da vírgula escrever o número 0.
Por exemplo, em vez de 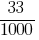escrever 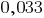(leem: "0 inteiros e 33 milésimos").

Preste atenção! Após a vírgula o numerador da fração deve ter tantos números quantos zeros no denominador.

Tabela de dígitos decimais

Decimal, como qualquer número, composto de algarismos (0,1,2,3,4,5,6,7,8,9).

O lugar de cada dígito no número importante: é o que define o bit de número.

Decimal consiste de uma parte inteira (todos os números antes da vírgula) e a parte fracionária (todos os dígitos após a vírgula).

Toda a parte decimal pode ser decomposta em partes também, como números naturais: unidades, dezenas, centenas, milhares e т. д.

A parte fracionária decimal dividido em partes assim: décimos (no denominador comum de fracções 10), centésimo (décimos (no denominador comum de frações de 100), em milhares (décimos (no denominador comum da fracção de 1000) e т. д.

A tabela de dígitos e você pode adicionar qualquer ajuste o número de colunas.

1. 1 º dígito após a vírgula — descarga de décimos,
2. 2 º dígito após a vírgula — descarga centésimos,
3. 3 º dígito após a vírgula — descarga de milésimos,
4. 4 º dígito após a vírgula — descarga milésimos dez sobretaxa,
5. 5 º dígito após a vírgula — descarga стотысячных,
6. 6 º dígito após a vírgula — descarga ppm,
7. 7 º dígito após a vírgula — descarga десятимиллионным,
8. 8 º dígito após a vírgula — descarga стомільйонних.

Adição e subtração de frações decimais

Para adicionar ou subtrair frações decimais, você precisa:

1. Equilibrar esses дробях o número de dígitos após a vírgula;
2. Gravá-los sob um do outro, para que a vírgula foi gravada sob o ponto e vírgula;
3. Executar a adição (subtração), não prestando atenção em vírgula;
4. Colocar na resposta de uma vírgula debaixo de vírgula dados дробях.

Exemplo:

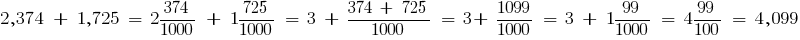
Propriedades da adição de frações decimais:

a + b = b + a - переставная propriedade

(a + b) + c = a + ( b + c ) - middleware propriedade

A multiplicação de frações decimais

Para multiplicar duas frações decimais, temos:
1. realizar a multiplicação, não prestando atenção nas vírgulas;
2. separar com vírgula tanto de dígitos à direita, quanto após a vírgula em ambos os multiplicadores junto.

Leia mais aqui

Divisão de frações decimais

Para compartilhar o decimal por um número natural, é necessário:
1. dividir uma fração deste número, ignorando a vírgula;
2. colocar em particular a vírgula, quando acabar o делення a parte inteira.

Leia mais aqui

Comparação de frações decimais

Para comparar duas frações decimais, primeiro devemos igualar a eles o número de casas decimais, atribuir a um deles zeros à direita, e então, deixando de lado a vírgula, comparar os resultantes números naturais.

Exemplo:

Compare as duas frações decimais 0,642 e 0,65. Уравняем o número de casas decimais, atribuir ao número de 0,65 negócio do zero. Obtemos a fração 0,564 e 0,650.

Gravá-los em forma de frações ordinárias:

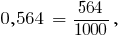
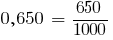
Nos denominadores das frações iguais.

A partir de duas frações com o mesmo знаменателями, mais uma fração, o que tem maior numerador.
Assim como 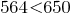, então 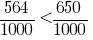, e, portanto,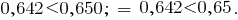

Frações decimais podem ser comparados e a estática.

Em decimais дробях 26,63 e 6,553 suficiente comparar os inteiros parte. Assim como ,;.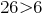

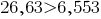Finais e infinitas frações decimais

Definição:oFinal de uma fração decimal é chamado de fração que contém o destino é o número de dígitos após o ponto decimal.

Exemplo: 222,35

Definição:o Infinito de uma fração decimal é chamado de fração, o que não contem o final do número de dígitos após o ponto decimal.

Exemplo: 222,35...

Definição:aInfinita periódica como um número decimal (periódica fração) é chamado de infinito fração, no final, contém um grupo de algarismos que se repetem.

Exemplo: 222,489898989...

O período de infinita periódica em fração decimal é um grupo de algarismos que se repetem. No exemplo anterior, é de 89.

Periódica decimal é chamado de limpa periodicamente a fração, se o seu período começa imediatamente após a vírgula e o período pode conter qualquer número finito de dígitos.

Exemplo: 8,44444....

Periódica decimal é chamado de fração mista, se a decimal um número, colocado entre toda a parte e o período. O número periódica em fração, ereto entre toda a parte e o período, chamado de передперіодом desta fração.

Exemplo: 8,4578787878...