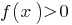Равносильные conversão mais simples de desigualdades
 Quando a > 1
Quando a > 1
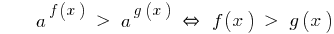
Sinal de desigualdade persiste.
Exemplo 1
Розвяжіть desigualdade: 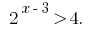
Solução:
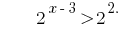
A função 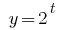 é crescente, portanto igualam indicadores,
é crescente, portanto igualam indicadores,
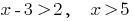
Resposta: 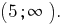
 Quando 0 < e < 1
Quando 0 < e < 1
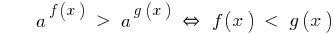
O sinal da desigualdade muda para o oposto.
Exemplo 2
Розвяжіть desigualdade: 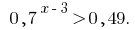
Solução:
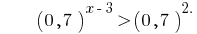
Função
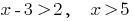
Resposta: 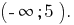
Enfrentar os desafios mais complexos inequações exponenciais
Com a ajuda de равносильных transformação
Com a ajuda de равносильных de transformação (em um esquema de resolver equações exponenciais) determinado a desigualdade se resume a desigualdade famoso forma (quadrada, o símbolo decimal ou outro). Após a solução obtida desigualdade chegamos a mais simples inequações exponenciais.
Exemplo 3
Розвяжіть desigualdade: 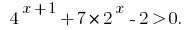
Solução:
Substituição 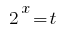 dá desigualdade
dá desigualdade 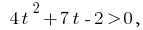
a dissociação que 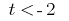 ou
ou 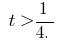
Então 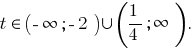
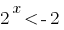 (розвязків não) ou
(розвязків não) ou 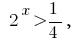 de onde
de onde 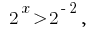 seja
seja 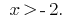
Resposta: 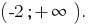
Utilizando o método de intervalos de
Aplicamos geral o método de intervalos,
- Encontrar ОДЗ
- Encontrar os zeros da função

- Notar os zeros da função no ОДЗ e encontrar o sinal
 em cada um dos períodos, em que é dividido ОДЗ.
em cada um dos períodos, em que é dividido ОДЗ. - Anotar a resposta, considerando-se o sinal da desigualdade.
Exemplo 4
Розвяжіть desigualdade: 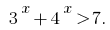
Solução:
Resolveremos a desigualdade método de intervalos. Definida a desigualdade івносильна irregularidades 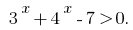
Vamos 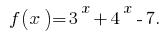
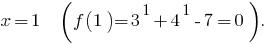
- ОДЗ:
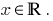
- Zeros de funções:
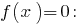
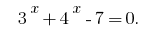
- Como a função
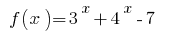 é crescente, o valor igual a zero, ela aceita apenas um ponto de escopo:
é crescente, o valor igual a zero, ela aceita apenas um ponto de escopo: - Vamos zero da função no ОДЗ, encontramos o sinal
 em cada um dos períodos, em que розбвається ОДЗ, e gravamos a dissociação irregularidades
em cada um dos períodos, em que розбвається ОДЗ, e gravamos a dissociação irregularidades 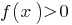
Resposta: 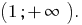
A solução de inequações é muito semelhante às equações exponenciais, portanto, se Você não encontrou o розязання adequados de irregularidades, vá para a página exponencial da equação.

 Quando a > 1
Quando a > 1
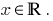
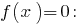
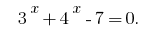
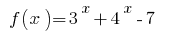 é crescente, o valor igual a zero, ela aceita apenas um ponto de escopo:
é crescente, o valor igual a zero, ela aceita apenas um ponto de escopo: