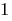Logarítmicas desigualdade

Definição: Logarítmica, a desigualdade — desigualdade, em que a variável está sob o signo de logaritmo.

Para um bom poder de розвязувати logarítmicas desigualdade, você deve ser capaz de manter os índices de logaritmo.

Равносильные conversão mais simples inequações logarítmicas.

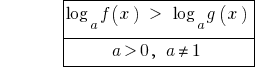
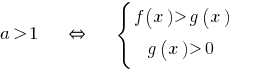
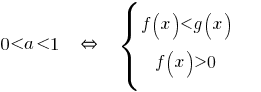
Quando o 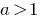sinal de desigualdade não se altera e é considerado ОДЗ.

Quando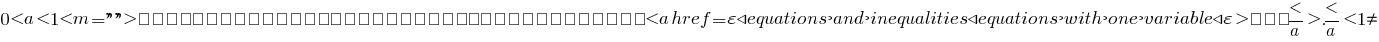

Exemplos de solução mais simples de equações logarítmicas

 

Exemplo 1

Розвяжіть equação: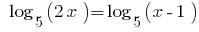

Solução:

Porque 5>1, então a função 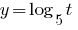— crescente e, considerando ОДЗ, obtemos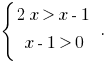

A partir daqui, 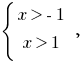ou seja,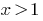

Resposta: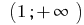

 

Exemplo 2

Розвяжіть equação: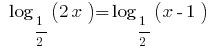

Solução:

Porque 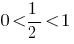, então a função 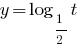— primeiro e, considerando ОДЗ, obtemos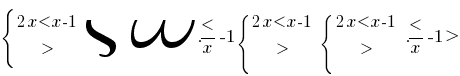

A partir daqui, 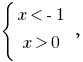— розвязків não.

Então 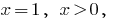isto é,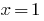

Resposta: розвязків não.

O esquema de enfrentar os desafios mais complexos de equações logarítmicas

1. O uso do método de intervalos de
2. O uso de transformações равносильных

Como розвязати logarítmica da equação

Com a ajuda de fórmulas логарифмирования e потенцирования redutível a equação a простейшему (neste caso consideramos ОДЗ inicial e seguindo para não perder as raízes quando звужуванні ОДЗ). Após a transformação, se não é possível reduzir mais simples logaritmico equação tentando introduzir a substituição de variáveis.

Exemplos de resolver inequações logarítmicas

 

Logarítmicas desigualdade розвязуються assim como e equações logarítmicas.

Exemplo 3 (utilização de fórmulas логарифмирования)

 

Розвяжіть equação: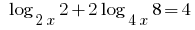

Solução:

Indo para a base 2, obtemos a equação равносильные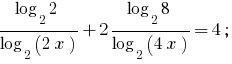

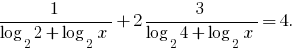
Substituição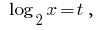

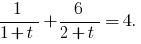
Então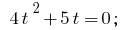

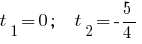
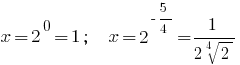
Resposta: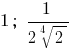

Exemplo 4 (usando as propriedades logarítmicas funções)

 

Розвяжіть equação: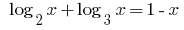

Solução:

O recurso 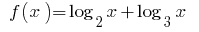aumenta a área de determinar como a soma de duas funções crescentes e 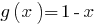vem. Assim definido, a equação tem uma única raiz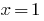

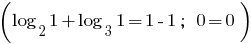
Resposta: