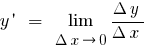
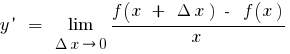
Definição:a Derivada de uma função 
em um ponto 
chamado de limite de uma relação de incremento da função no ponto mudou para o incremento do argumento, quando o incremento do argumento tende a zero (pode indicar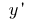 
ou 
)
A operação de encontrar a derivada é chamado de diferenciação
O conceito de ganho de argumento e função
Aumento do argumento
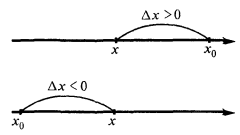
O incremento de funções
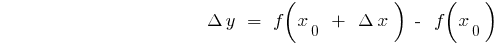
Derivadas de funções elementares
Derivadas de funções elementares estão usando a tabela:
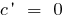
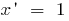
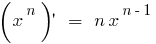
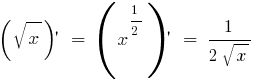
Todos os derivados básicos de funções, você pode encontrar aqui!
É compor de uma função. Como encontrar a função composta
Derivada da soma (diferença) de duas funções, cada um dos quais tem uma derivada é igual a soma (diferença) dos derivados destas funções:
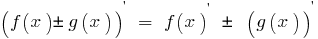
O derivado de obras de duas funções, cada um dos quais tem uma derivada é igual à soma dos trabalhos de cada função para a derivada segunda da função:
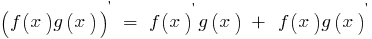
Derivada de uma quota de participação de duas funções f(x) e g(x), cada um dos quais tem uma derivada e g(x)≠0, encontrar a fórmula
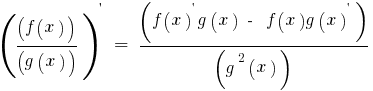
Permanente de multiplicador você pode passar atrás do sinal da derivada:
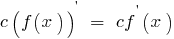
As fórmulas chamam de regras de diferenciação.
O significado geométrico da derivada
A tangente à curva neste ponto 
chamado de limite de posição секущей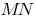 
, quando o ponto 
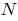se aproxima ao longo da curva, a ponto de
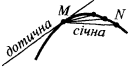
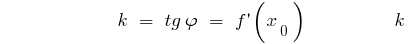o declive da tangente
A equação da tangente ao gráfico da função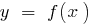 
no ponto de абцисою 
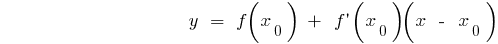
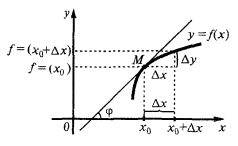
O valor da derivada no ponto a é igual canto marcado relação da tangente ao gráfico da função no ponto de абцисою e é igual a тангенсу o ângulo de inclinação desta tangente ao eixo 
O significado físico de um derivado
Derivado caracteriza a velocidade de mudança de função quando você altera o argumento
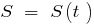— a dependência do caminho percorrido, do tempo do
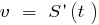— a velocidade de movimento linear
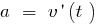— aceleração de movimento linear