Definição: um Número 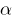 é chamado de raiz de polinômio
é chamado de raiz de polinômio  , se
, se 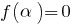 (т. е.
(т. е. 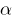 é a raiz de uma equação
é a raiz de uma equação  )
)
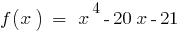 . O número 3 é a raiz de polinômio, porque
. O número 3 é a raiz de polinômio, porque 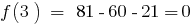
O mais simples, as propriedades das raízes
Porque a 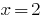 raiz de polinômio
raiz de polinômio 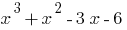 , então este polinômio é dividido em
, então este polinômio é dividido em 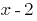 ;
;
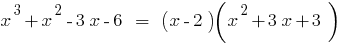
- Se o número
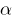 é raiz do polinômio
é raiz do polinômio  , então este polinômio é dividido em двочлен
, então este polinômio é dividido em двочлен 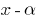 sem deixar resíduos — uma conseqüência do teorema de Bézout;
sem deixar resíduos — uma conseqüência do teorema de Bézout; - Um polinômio de grau
 não pode ter mais
não pode ter mais  raízes;
raízes; - Se para o polinômio
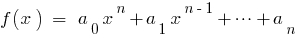 de ti sabemos
de ti sabemos  de suas raízes:
de suas raízes: 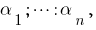 este polinômio pode ser decomposto em multiplicadores assim:
este polinômio pode ser decomposto em multiplicadores assim: 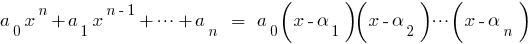 .
.
A Fórmula Виета
Se 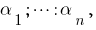 — as raízes do polinômio
— as raízes do polinômio 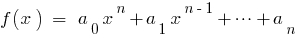 , então comparando os coeficientes iguais graus
, então comparando os coeficientes iguais graus  para a esquerda e para a direita, obtemos a relação entre as raízes de polinômio e seus coeficientes, que são chamados de fórmulas Вієти.
para a esquerda e para a direita, obtemos a relação entre as raízes de polinômio e seus coeficientes, que são chamados de fórmulas Вієти.
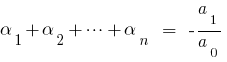
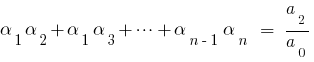
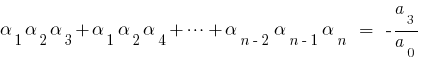
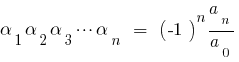
Quando é 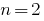 para o quadrado de трехчлена
para o quadrado de трехчлена 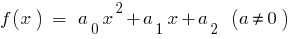 temos
temos
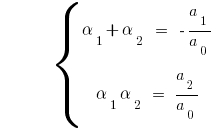
Quando 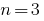 para cúbicos de трехчлена
para cúbicos de трехчлена 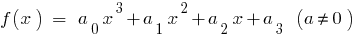 temos
temos
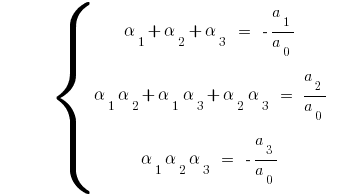

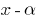 sem deixar resíduos — uma conseqüência do
sem deixar resíduos — uma conseqüência do  não pode ter mais
não pode ter mais 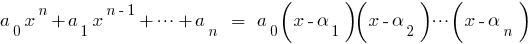 .
.