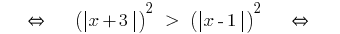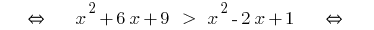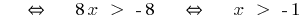Definição: a Desigualdade a partir de uma variável, 
duas expressões de uma variável de estados de um sinal de 
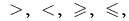que, em geral, como é escrito assim: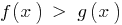 
Definição: a Raiz (ou розвязком) a desigualdade é um valor variável, que transforma a desigualdade na certa igualdade numérica.
Розвязати desigualdade — significa encontrar todas as suas raízes (dissociação) ou mostrar o que não são.
O intervalo de valores permitidos ОДЗ desigualdade
Definição: o intervalo de valores permitidos (escopo) irregularidades — área total de definição de funções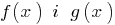 
, em pé no lado esquerdo e direito da equação.
Encontrar o intervalo de valores permitidos (ОДЗ)
Exemplo
Definida a equação: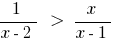 
ОДЗ: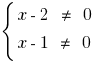 
, т. е.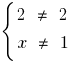 
o que você pode gravar e assim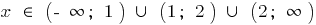 
.
Irregularidades — consequências
Quando розвязувнні irregularidades consequências não são usadas (e são usados равносильные de conversão), pois, normalmente, não é possível verificar todas as denúncias розвязків desigualdade-efeito.
Равносильные desigualdade
Definição: Elevaram - (são equivalentes) as irregularidades ou duas irregularidades, que em muitos ОДЗ têm os mesmos de dissociação, ou seja, cada decisão de primeira desigualdade é розвязком de um segundo e vice-versa.
Alguns teoremas sobre равносильности equações
Teorema 1: Se a partir de uma parte da desigualdade de transferir para outra parte do soma com o sinal oposto, teremos нерівнсть, равносильное especificado (em qualquer conjunto).
Teorema 2.1: Se ambas as partes desigualdade multiplicar ou dividir por um mesmo número positivo, diferente de zero (ou para a mesma função, que é definida e não igual a zero no ОДЗ especificado equação), obtemos a desigualdade равносильное especificado.
Teorema 2.2: Se ambas as partes desigualdade multiplicar ou dividir uma mesma відємне número diferente de zero (ou para a mesma função, que é definida e відємна em ОДЗ especificado equação) e, krm disso, trocar o sinal de desigualdade oposta, obtemos a desigualdade, равносильное especificado.
Teorema 3.1: Se de ambas as partes desigualdade 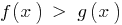assumir cada vez mais uma função 
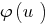(mantendo o sinal de desigualdade) e quando isso não ocorre o estreitamento de ОДЗ especificado desigualdade, recebida a desigualdade 
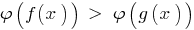é equivalente especificado (no ОДЗ).
Teorema 3:2 Se de ambas as partes desigualdade 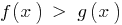tomar uma trajetória de recurso 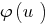, alterando o sinal de desigualdade, e quando isso não ocorre o estreitamento de ОДЗ especificado desigualdade, recebida a desigualdade 
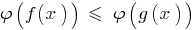é equivalente especificado (no ОДЗ).
A investigação do teorema sobre a равносильности desigualdades
Resultado: Como a função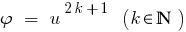 
monótona crescente,o
.
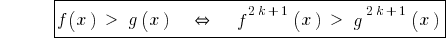Quando поднесении de ambas as partes até estranho natural grau obtemos a desigualdade, равносильное a esta.
Resultado: Como a função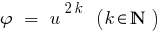 
monotonamente aumenta apenas quando 
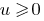,no caso, quando ambas as partes desigualdade невідємні, durante a elevação de ambas as partes, até mesmo natural grau obtemos нерінвість, равносильное a esta.
Exemplo 1
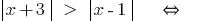(ambas as partes невідємні!)
