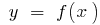Exemplo. 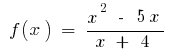
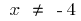
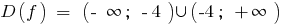
A função nem par nem ímpar e periódica
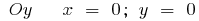
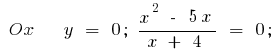
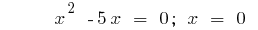 ou
ou 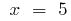
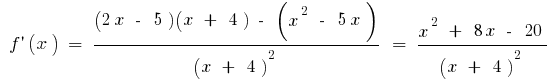
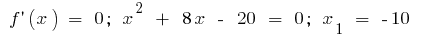 ou
ou 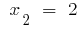
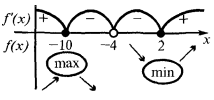
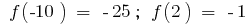
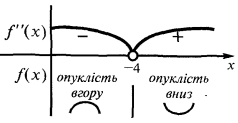
Encontrar o ponto de inflexão (se existirem) e o valor  em pontos de inflexão
em pontos de inflexão
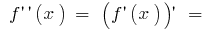
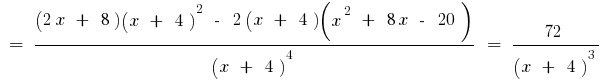
Assim, 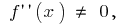 o sinal da segunda derivada pode variar apenas no ponto
o sinal da segunda derivada pode variar apenas no ponto 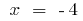
- A definição da área
- Paridade, a estranheza, a frequência de
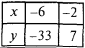
- A intersecção com os eixos de coordenadas
- O derivado e pontos críticos
- Intervalos de ascendente, descendente e ponto de extremo (e os valores de função nesses pontos)
- O comportamento da função para as extremidades da área de definição e os asymptotes gráfico da função (verticais, horizontais e inclinadas)
Quando
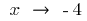 a esquerda
a esquerda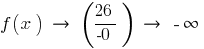
Quando
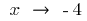 o negócio
o negócio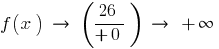
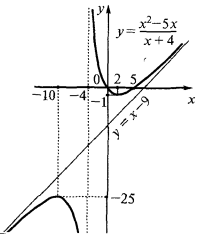
Portanto,
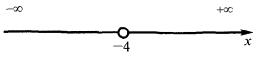
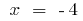 — vertical асимптота
— vertical асимптотаPorque
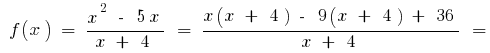
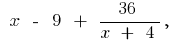 então, quando
então, quando 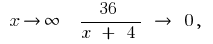 então
então 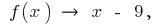 т. е.
т. е. 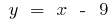 — a inclinação é асимптота
— a inclinação é асимптота - A segunda derivada e o estudo de funções no bojo e угнутість
- Se precisa encontrar os pontos de verificação, melhoria do comportamento gráfico
- Com base na pesquisa, construímos um esboço do gráfico da função
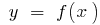


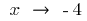 a esquerda
a esquerda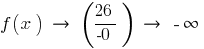
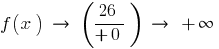
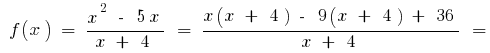
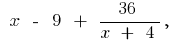 então, quando
então, quando 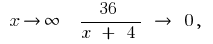 então
então 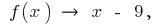 т. е.
т. е. 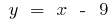 — a inclinação é асимптота
— a inclinação é асимптота