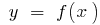Приклад. 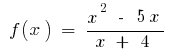
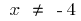
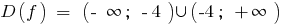
Функція ні парна, ні непарна і не періодична
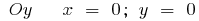
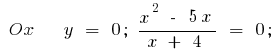
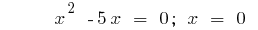 або
або 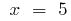
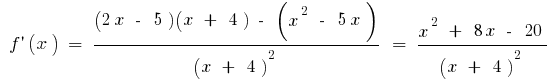
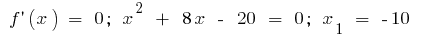 або
або 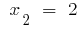
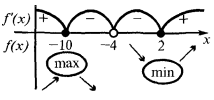
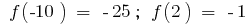
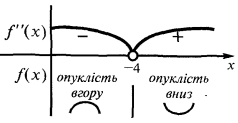
Знайти точки перегину (якщо вони існують) і значення  в точках перегину
в точках перегину
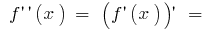
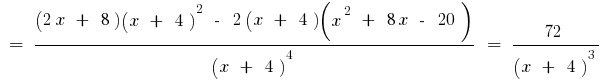
Оскільки 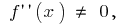 то знак другої похідної може змінюватися лише в точці
то знак другої похідної може змінюватися лише в точці 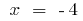
- Область визначення
- Парність, непарність, періодичність
- Перетин з осями координат
- Похідна і критичні точки
- Проміжки зростання, спадання і точки екстремуму (і значення функції в цих точках)
- Поведінка функції на кінцях області визначення і асимптоти графіка функції (вертикальні, горизонтальні і похилі)
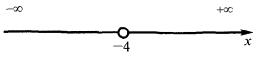
При
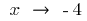 зліва
зліва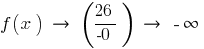
При
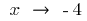 справа
справа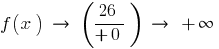
Отже,
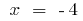 — вертикальна асимптота
— вертикальна асимптотаОскільки
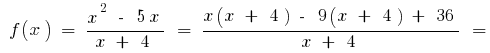
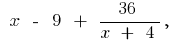 то при
то при 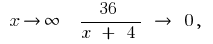 тоді
тоді 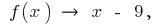 тобто
тобто 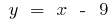 — похила асимптота
— похила асимптота - Друга похідна і дослідження функції на опуклість і угнутість
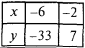
- Якщо необхідно, знайти контрольні точки, що уточнюють поведінку графіка
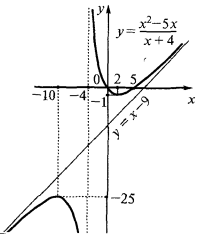
- На основі проведеного дослідження будуємо ескіз графіка функції
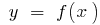


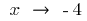 зліва
зліва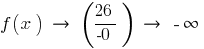
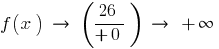
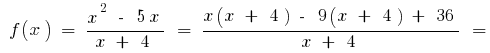
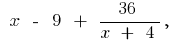 то при
то при 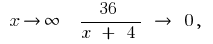 тоді
тоді 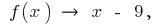 тобто
тобто 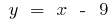 — похила асимптота
— похила асимптота