Означення: Асимптота кривої — це пряма, до якої необмежено наближається крива при видаленні іі в нескінечність.
Вертикальні асимптоти 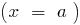
 — вертикальна асимптота,
— вертикальна асимптота,  при
при 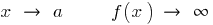
Вертикальна асимптота  може бути в точці
може бути в точці  , якщо точка
, якщо точка  обмежує відкриті проміжки області визначення даної функції і біля точки
обмежує відкриті проміжки області визначення даної функції і біля точки  функція прямує до нескінечності.
функція прямує до нескінечності.
Приклади вертикальних асимптот
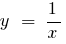
При 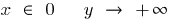
При 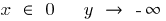
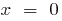 — вертикальна асимптота
— вертикальна асимптота
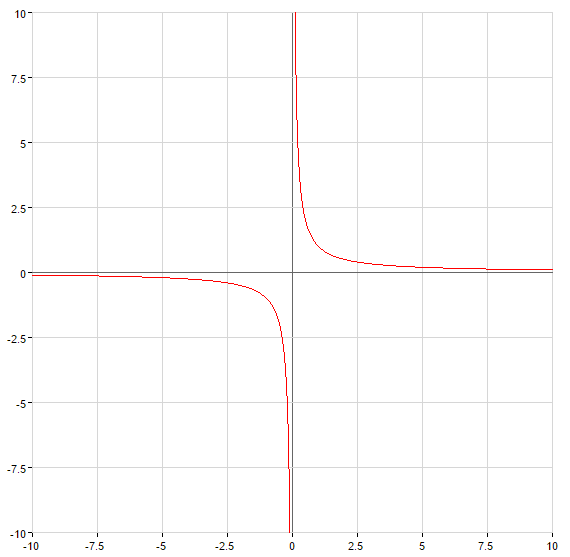
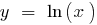
При 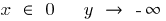
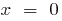 — вертикальна асимптота
— вертикальна асимптота
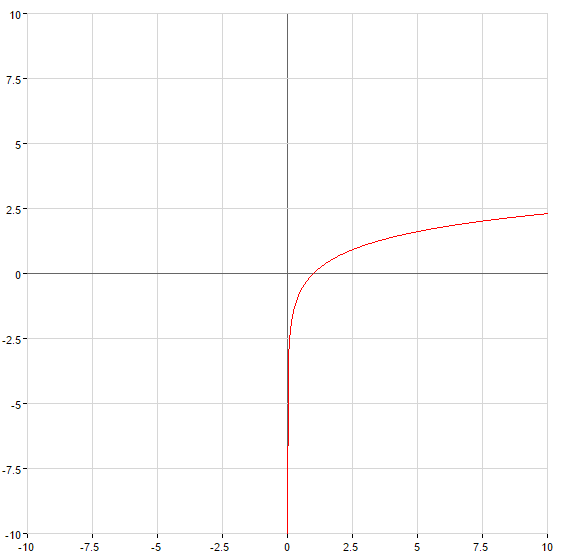
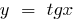
При 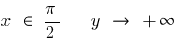
При 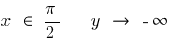
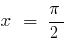 — вертикальна асимптота
— вертикальна асимптота
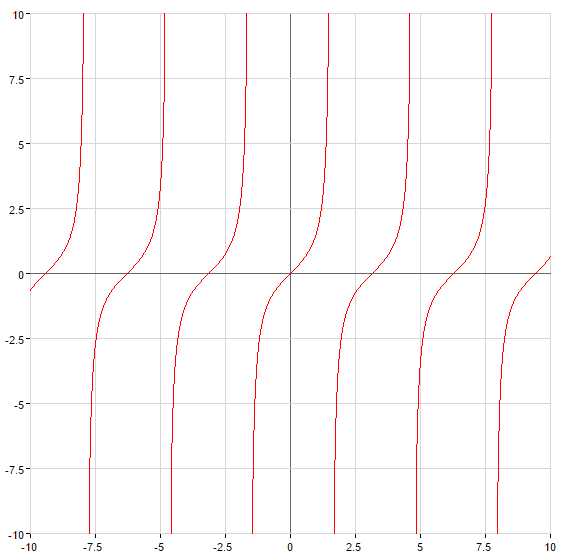
Похилі і горизонтальні асимптоти 

- Якщо
 — дробово-раціональна функція, в якій степень чисельника на одиницю більший від степеня знаменника, то виділяємо цілу частину і використовуємо означення асимптоти.
— дробово-раціональна функція, в якій степень чисельника на одиницю більший від степеня знаменника, то виділяємо цілу частину і використовуємо означення асимптоти. - У загальному випадку рівняння похилих і горизонтальних асимптот
 можуть бути одержані з використанням формул
можуть бути одержані з використанням формул

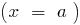
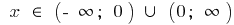
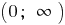
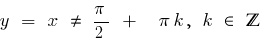

 — дробово-раціональна функція, в якій степень чисельника на одиницю більший від степеня знаменника, то виділяємо цілу частину і використовуємо означення асимптоти.
— дробово-раціональна функція, в якій степень чисельника на одиницю більший від степеня знаменника, то виділяємо цілу частину і використовуємо означення асимптоти.