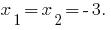Квадратне рівняння, теорема Вієта

Квадратні рівняння

Означення: Квадратне рівняння — рівняння вигляду 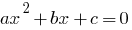, де 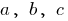— деякі числа, причому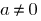

Квадратне рівняння загального виду

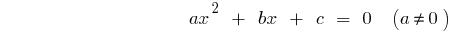
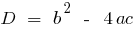— дискримінант квадратного рівняння

 

 

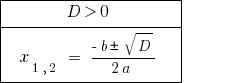
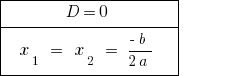
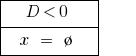
При 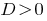— рівняння має два різних корені.

При — рівняння має два рівних корені. При підрахунку кількості розвязків вважається за одне значення кореня.

При 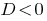— рівняння коренів немає.

Зведене рівняння (а = 1)

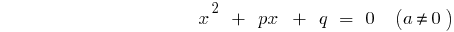
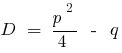— дискримінант зведеного рівняння

 

 

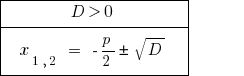
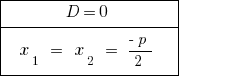
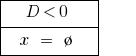
При 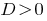— зведене рівняння має два різних корені.

При — зведене рівняння має два рівних корені. При підрахунку кількості розвязків вважається за одне значення кореня.

При 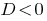— зведене рівняння коренів немає.

Теорема Вієта у загальному випадку

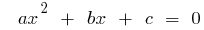Якщо — корені квадратного рівняння , то

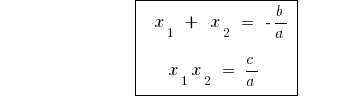
Теорема Вієта для зведеного рівняння (a=1)

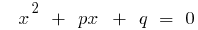Якщо — корені зведеного квадратного рівняння , то

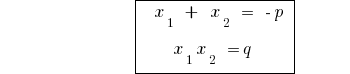
Обернена теорема до теореми Вієта

Теорема: Якщо сума двох чисел дорівнює 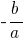, а добуток дорівнює 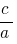, то ці числа є коренями квадратного рівняння .

 

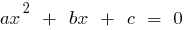Теорема (для зведеного рівняння): Якщо сума двох чисел дорівнює 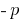, а добуток дорівнює 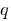, то ці числа є коренями квадратного рівняння .

 

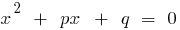Розкладання квадратного тричлена на множники

Якщо — корені квадратного тричлена дорівнює нулю 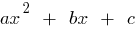(тобто корені рівняння 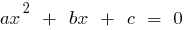), то

 

 

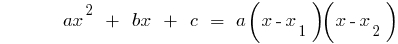
Якщо дискримінант квадратного тричлена дорівнює нулю (), то 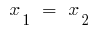, і тоді

 

 

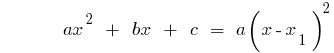
Приклад. Розкладання тричлена на множники

1. при
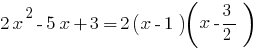
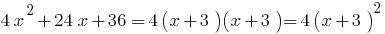
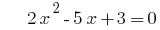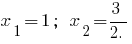
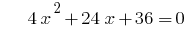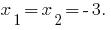
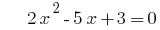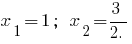
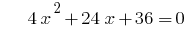2. при