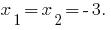Quadratische Gleichung, Theorem vieta

Quadratische Gleichungen

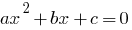Definition: Quadratische Gleichung — Gleichung der Art , wo 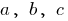— einige zahlen, wobei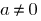

Eine quadratische Gleichung der Allgemeinen Form

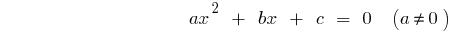
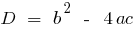— дискриминантов quadratische Gleichung

 

 

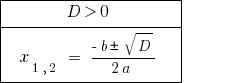
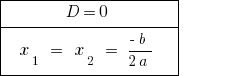
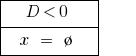
Bei 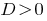— Gleichung hat zwei verschiedene Wurzeln.

Bei der — Gleichung hat zwei gleiche Wurzel. Bei der Berechnung der Anzahl der розвязків gilt als ein Wert der Wurzel.

Bei 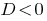— Gleichung keine Wurzeln.

Pivot-Gleichung (a = 1)

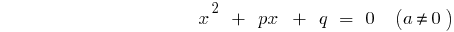
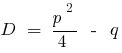— дискриминантов zusammenfassenden Gleichungen

 

 

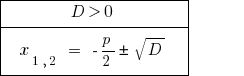
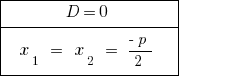
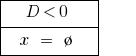
Bei 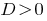— Pivot-Gleichung hat zwei verschiedene Wurzeln.

Bei — Pivot-Gleichung hat zwei gleiche Wurzel. Bei der Berechnung der Anzahl der розвязків gilt als ein Wert der Wurzel.

Bei 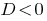— Pivot-Gleichung keine Wurzeln.

Das Theorem im Allgemeinen Fall vieta

Wenn die Wurzeln einer quadratischen Gleichung 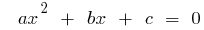, dann

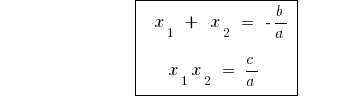
Theorem vieta für einen zusammenfassenden Gleichung (a=1)

Wenn — die Wurzeln der konsolidierten quadratischen Gleichung 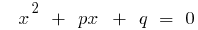, dann

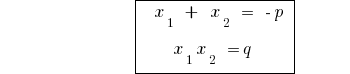
Inverse Theorem Theorem vieta

Theorem: Wenn die Summe der beiden zahlen ist gleich 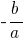, und das Produkt gleich 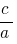, dann werden diese zahlen sind die Wurzeln einer quadratischen Gleichung .

 

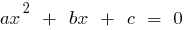Theorem (für die zusammengefassten Gleichungen): Wenn die Summe der beiden zahlen ist gleich 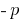, und das Produkt gleich 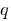, dann werden diese zahlen sind die Wurzeln einer quadratischen Gleichung .

 

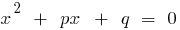Aufspaltung quadratischen трехчлена auf Multiplikatoren

Wenn — die Wurzeln der quadratischen трехчлена gleich null 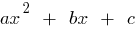(D. H. die Wurzeln der Gleichung 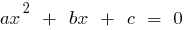), dann

 

 

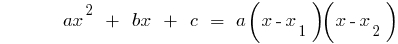
Wenn дискриминантов quadratischen трехчлена gleich null ist (), dann 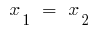, und dann

 

 

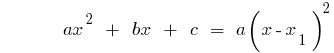
Beispiel. Die ZERLEGUNG auf dem Faktor трехчлена

1. bei
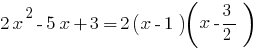
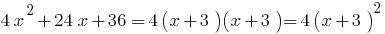
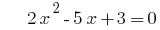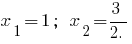
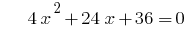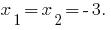
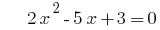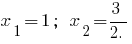
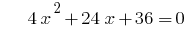2. bei