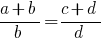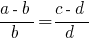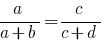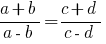Definition: Anteil nennt man die Gleichheit der beiden Beziehungen.
oder 
.
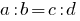Die wichtigste Eigenschaft der Proportionen
Werk extrem Mitglieder Mitglieder der proportion ist gleich dem Produkt Ihrer durchschnittlichen Mitglieder: wenn
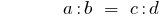dann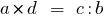 
Eigenschaften der Proportionen
- Werk extrem Mitglieder Mitglieder der proportion ist gleich dem Produkt Ihrer durchschnittlichen Mitglieder:
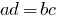. - Jedes Mitglied ganz proportion ist gleich dem Produkt Ihrer durchschnittlichen Mitglieder, geteilt durch den ein anderes Mitglied ganz.
- In jedem Verhältnis kann man vertauschen oder nur die mittleren Glieder oder Extreme, oder auch jener, und andere gleichzeitig.
.Beispiel des Verbleibs Anteil in der Mathematik
Wenn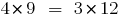 
, dann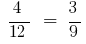 
Im Verhältnis 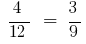zu ändern stellenweise Mitglieder der mittlere oder Extreme Mitglieder, dann bekommen wir wieder die richtigen Gleichheit:
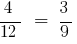und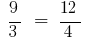 
Abgeleitete Proportionen
Wenn die angegebene Anteil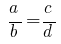 
, das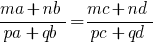 
, was als abgeleitete Anteil.
Die am häufigsten verwendeten Derivate Proportionen
Maßstab
Definition: Maßstab — das Verhältnis des Abstands auf der Karte zur entsprechenden Entfernung auf dem eigentlichen Gelände.
Direkt proportionale Größen
Definition: Zwei Werte heißen direkt proportional, wenn mit Zunahme der Werte einer von Ihnen mehrmals einen anderen Wert steigt um den gleichen Faktor.
Aufgaben auf direkt proportionale Größen
Seite des Quadrats beträgt 3 DM. Wie ändert sich der Umfang des Quadrats, wenn seine Seite erhöhen 3 mal, 4 mal, 5 mal?
Seite des Platzes 3 DM, Umfang 12 DM
Seite Quadrat 9 DM, Umfang 36 DM
Seite des Platzes 12 DM, Umfang 48 DM
Seite des Platzes 15 DM, Umkreis von 60 DM
Bei der Vergrößerung der Seite eines Quadrats in 3 mal (war 3 DM, war — 9 DM), der Umfang stieg auch 3 mal (war 9 DM, wurde — 36 DM).
Ebenso bei der Vergrößerung der Seitenlänge des Quadrats ist 4-mal (war 3 DM, war — 12 DM), der Umfang stieg auch 4 mal (war 12 DM, wurde — 48 DM).
Fazit: bei der Vergrößerung des Platzes mehrmals, der Umfang steigt um den gleichen Faktor.
Seite des Quadrats direkt proportional zu seinem Umfang.
Zurück proportionale Größen
Definition: Zwei Werte werden als обенено proportional, wenn mit Zunahme der Werte einer von Ihnen mehrmals einen anderen Wert verringert sich um den gleichen Faktor.
Aufgaben wieder auf proportionale Größen
Der Abstand zwischen den zwei Ortschaften noch 160 km in welcher Zeit erreichen Sie von einem Dorf zum anderen, wenn die Geschwindigkeit 10 km/h erhöhen 2 mal, 4 mal, 8 mal?
Geschwindigkeit, km/h 10 Zeit, h 16
Geschwindigkeit, km/h 20 Zeit, h 8
Geschwindigkeit, km/h 40 Zeit, h 4
Geschwindigkeit, km/h 80 Zeit, h 2
Durch die Erhöhung der Geschwindigkeit in 2 mal (war 10 km/h — 20 km/h), Zeit zurückgegangen (gesunken) 2 mal (war 16 h, war — 8 Stunden).
Auch bei der Erhöhung der Geschwindigkeit 4-mal (war 10 km/h — 40 km/h), Zeit zurückgegangen (gesunken) 4-mal (16 h wurde 4 Stunden).
Fazit: bei einer Steigerung der Geschwindigkeit in ein paar mal, Zeit verringert sich in der gleichen Zeit.
Die Geschwindigkeit Umgekehrt proportional zur Zeit.
Zahlen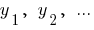 
proportionale zahlen 
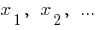, wenn 
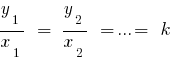— Koeffizient der Verhältnismäßigkeit.
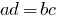